Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

Why you only need 23 people for a 50% chance of a shared birthday

Here’s a counterintuitive fact: in a room of just 23 people, there’s a better than 50% chance that two of them share a birthday. With 70 people, it’s virtually certain (99.9%). Let’s build up to understanding why, starting from the simplest case.

The Clever Trick: Complement Counting

Directly counting all the ways people could share birthdays is messy — you’d have to consider pairs sharing, triplets sharing, different combinations... Instead, we flip the problem:

P(at least 2 share a birthday)=1−P(no one shares a birthday)P(\text{at least 2 share a birthday}) = 1 - P(\text{no one shares a birthday})
(1)

Calculating “no shared birthdays” is surprisingly elegant. We just need everyone to pick different days. Let’s build this up person by person.

Case 1: Just One Person

With only one person, there’s no one to share a birthday with!

P(no shared birthday)=1P(\text{no shared birthday}) = 1
(2)
P(at least 2 share)=0P(\text{at least 2 share}) = 0
(3)

They can pick any of the 365 days — all options are “safe.”

<Figure size 1000x400 with 1 Axes>

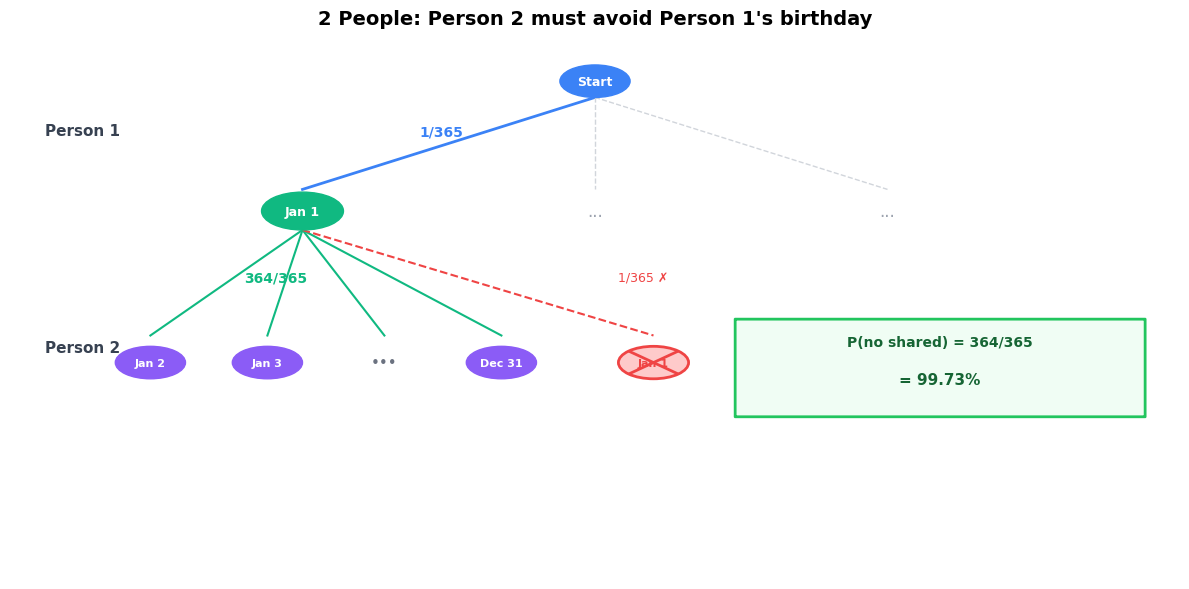
Case 2: Two People

Now it gets interesting. Person 1 picks any day. Person 2 must pick a different day to avoid a collision.

P(no shared birthday)=365365×364365=364365≈0.9973P(\text{no shared birthday}) = \frac{365}{365} \times \frac{364}{365} = \frac{364}{365} \approx 0.9973
(4)
P(at least 2 share)=1−0.9973=0.27%P(\text{at least 2 share}) = 1 - 0.9973 = 0.27\%
(5)
<Figure size 1200x600 with 1 Axes>

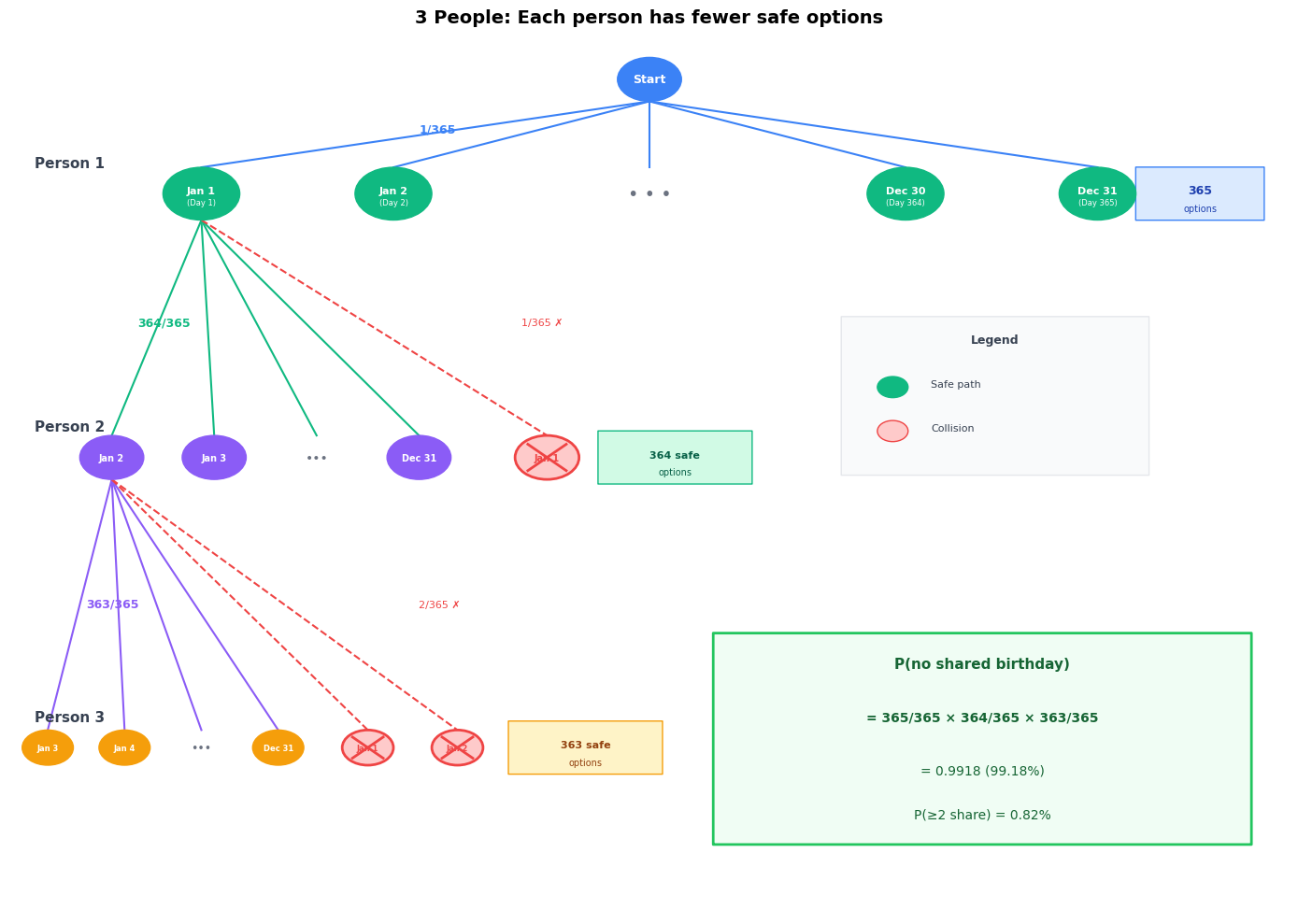
Case 3: Three People

Person 3 joins. Now they must avoid two birthdays.

P(no shared birthday)=365365×364365×363365≈0.9918P(\text{no shared birthday}) = \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \approx 0.9918
(6)
P(at least 2 share)=1−0.9918=0.82%P(\text{at least 2 share}) = 1 - 0.9918 = 0.82\%
(7)
<Figure size 1400x1000 with 1 Axes>

The Pattern Emerges

Notice what’s happening:

The General Case: N People

For n people, the pattern continues:

P(no shared birthday)=365365×364365×363365×⋯×365−n+1365P(\text{no shared birthday}) = \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \cdots \times \frac{365-n+1}{365}
(8)

Or more compactly using product notation:

P(no shared birthday)=∏k=0n−1365−k365=365!(365−n)!⋅365nP(\text{no shared birthday}) = \prod_{k=0}^{n-1} \frac{365-k}{365} = \frac{365!}{(365-n)! \cdot 365^n}
(9)

What does ∏ mean? The symbol ∏\prod (capital Greek letter “pi”) means “product” — multiply all the terms together. It’s like ∑\sum (summation), but for multiplication instead of addition. Here, ∏k=0n−1\prod_{k=0}^{n-1} means “multiply the expression for each value of k from 0 to n-1.”

From Product to Factorial

Here’s how to get from product notation to factorial form:

Step 1: Separate the numerators and denominators (n fractions, so n terms each):

∏k=0n−1365−k365=365×364×363×⋯×(365−n+1)365×365×365×⋯×365=365×364×⋯×(365−n+1)365n\prod_{k=0}^{n-1} \frac{365-k}{365} = \frac{365 \times 364 \times 363 \times \cdots \times (365-n+1)}{365 \times 365 \times 365 \times \cdots \times 365} = \frac{365 \times 364 \times \cdots \times (365-n+1)}{365^n}
(10)

Step 2: Recognize the numerator as a “falling factorial” — it’s 365!365! with the smaller terms cut off:

365×364×⋯×(365−n+1)=365!(365−n)!365 \times 364 \times \cdots \times (365-n+1) = \frac{365!}{(365-n)!}
(11)

This works because 365!=365×364×⋯×(365−n+1)×(365−n)×⋯×1365! = 365 \times 364 \times \cdots \times (365-n+1) \times (365-n) \times \cdots \times 1, and dividing by (365−n)!(365-n)! cancels the tail.

Step 3: Combine:

P(no shared birthday)=365!(365−n)!⋅365nP(\text{no shared birthday}) = \frac{365!}{(365-n)! \cdot 365^n}
(12)

Let’s see how this grows:

PeopleP(no shared)P(≥2 share)
299.73%0.27%
399.18%0.82%
597.29%2.71%
1088.31%11.69%
1574.71%25.29%
2058.86%41.14%
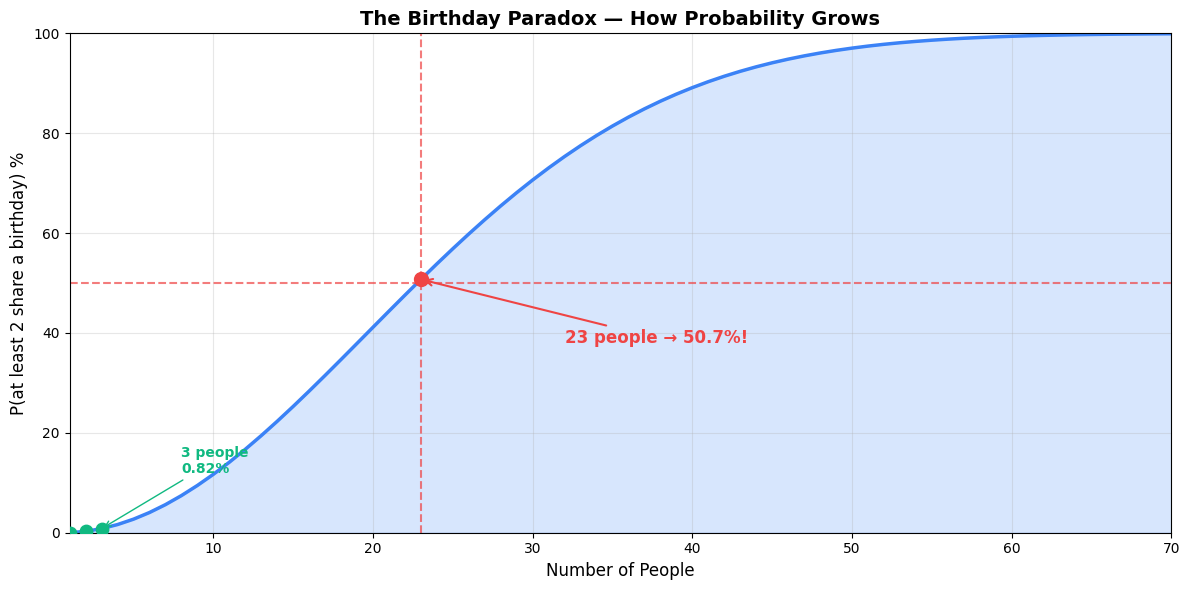
2349.27%50.73% ← 50%!
3029.37%70.63%
4010.88%89.12%
502.96%97.04%
700.08%99.92%

The probability rises fast. Let’s visualize this:

<Figure size 1200x600 with 1 Axes>

Why Is It So Counterintuitive?

Our intuition fails because we think about the wrong question. We instinctively imagine:

“What’s the chance someone shares my birthday?”

That probability is low — about 6% with 23 people. Here’s why: each of the other 22 people has a 364/365 chance of not matching your birthday, so:

P(someone matches mine)=1−(364365)22≈0.059=5.9%P(\text{someone matches mine}) = 1 - \left(\frac{364}{365}\right)^{22} \approx 0.059 = 5.9\%
(13)

But the birthday paradox asks a fundamentally different question:

“What’s the chance any two people share a birthday?”

The key difference: you’re no longer special. We’re not anchoring on one person’s birthday — we’re checking every possible pair.

The Power of Pairs

With 23 people, there are:

(232)=23×222=253 possible pairs\binom{23}{2} = \frac{23 \times 22}{2} = 253 \text{ possible pairs}
(14)

Each pair is an independent opportunity for a match. Think of it like buying lottery tickets:

While the pairs aren’t truly independent (they overlap in people), the intuition holds: more pairs = more chances for a collision.

The Exponential Trap

Here’s another way to see it. The probability of no match drops with each person:

PeoplePairsP(no shared)
2199.7%
104588.3%
2325349.3%
3043529.4%

The pairs grow quadratically (n² growth), while our intuition thinks linearly (n growth). That’s the heart of the paradox — we underestimate how fast opportunities for coincidence multiply.

Common Mistake to Avoid

When computing the probability, keep the denominator as 365 throughout. A common error is writing:

1365×1364×1363✗ WRONG\frac{1}{365} \times \frac{1}{364} \times \frac{1}{363} \quad \text{✗ WRONG}
(15)

But each person always chooses from 365 possible days. The shrinking numerator (365, 364, 363...) counts how many of those choices are “safe.”

365365×364365×363365✓ CORRECT\frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \quad \text{✓ CORRECT}
(16)

Summary

The birthday paradox isn’t really a paradox — just a demonstration of how quickly combinatorial possibilities grow.

Key insights:

  1. Use complement counting — Calculate P(none share) and subtract from 1

  2. Build up person by person — Each new person narrows the safe choices by one

  3. Multiply the probabilities — P(all different) = product of individual “safe” probabilities

  4. Pairs grow quadratically — n people create n(n-1)/2 pairs, which is why probability rises so fast

Now you understand why, in a typical classroom of 30 students, there’s a 70% chance two people share a birthday!

Probability
The Inclusion-Exclusion Principle
Neural Networks From Scratch
NN01 - Edge Detection Intuition: A Single Neuron as Pattern Matching