NN03 - Building a Flexible Neural Network from Scratch

Generalize from a fixed architecture to any number of layers

In NN02 - Training an Edge-Detection Neural Network from Scratch, we built a 2-layer edge detector with hardcoded weights W1, W2. But what if we want 3 layers? Or 10?

This tutorial shows how to generalize that code into a flexible architecture where you can specify any layer sizes. We’ll build a clean Layer class that handles forward and backward passes, then stack them together.

Prerequisites: You should understand the concepts from the previous tutorial (forward pass, backpropagation, gradient descent).

Goal: A ~100-line neural network that can handle arbitrary architectures like [784, 128, 64, 10] (for MNIST) or [25, 8, 2] (our edge detector).

import logging
import numpy as np
import warnings

logging.getLogger("matplotlib.font_manager").setLevel(logging.ERROR)
warnings.filterwarnings("ignore", message="Matplotlib is building the font cache*")

import matplotlib.pyplot as plt
np.random.seed(42)

The Problem with Hardcoded Layers¶

In our previous edge detector, we had:

# Hardcoded 2-layer network
W1 = np.random.randn(25, 8) * 0.3
b1 = np.zeros((1, 8))
W2 = np.random.randn(8, 2) * 0.3
b2 = np.zeros((1, 2))

And the forward/backward passes explicitly referenced W1, W2, z1, h1, etc.

What if we want 3 layers? We’d need to add W3, b3, z3, h3, and update all the forward/backward code.

The solution: Treat each layer as an object that knows how to:

Forward: Take input, produce output
Backward: Take gradient from above, compute gradient for weights and pass gradient below

The Layer Class¶

Each layer stores its own weights and handles its own forward/backward computation.

Linear Layer (Dense/Fully Connected)¶

A linear layer computes: $\mathbf{z} = \mathbf{x} W + \mathbf{b}$

Forward: Store input (needed for backward), compute output
Backward: Compute gradients for W and b, return gradient for input

class Linear:
    """Fully connected layer: z = x @ W + b"""
    
    def __init__(self, in_features, out_features):
        # Initialize weights (He initialization for ReLU)
        self.W = np.random.randn(in_features, out_features) * np.sqrt(2.0 / in_features)
        self.b = np.zeros((1, out_features))
        
        # Gradients (computed in backward)
        self.dW = None
        self.db = None
        
        # Cache for backward pass
        self.x = None
    
    def forward(self, x):
        self.x = x  # Cache input for backward
        return x @ self.W + self.b
    
    def backward(self, dz):
        """
        dz: gradient of loss w.r.t. this layer's output (shape: batch × out_features)
        Returns: gradient of loss w.r.t. this layer's input (shape: batch × in_features)
        """
        # Gradient for weights: dL/dW = x.T @ dL/dz
        self.dW = self.x.T @ dz
        
        # Gradient for bias: dL/db = sum over batch
        self.db = np.sum(dz, axis=0, keepdims=True)
        
        # Gradient for input: dL/dx = dL/dz @ W.T
        dx = dz @ self.W.T
        return dx
    
    def update(self, lr):
        """Update weights using gradient descent"""
        self.W -= lr * self.dW
        self.b -= lr * self.db

print("Linear layer: z = x @ W + b")
print("  forward(x)  -> stores x, returns z")
print("  backward(dz) -> computes dW, db, returns dx")

Linear layer: z = x @ W + b
  forward(x)  -> stores x, returns z
  backward(dz) -> computes dW, db, returns dx

ReLU Activation¶

ReLU computes: $h = \max(0, z)$

It has no learnable parameters, but still needs to pass gradients through.

class ReLU:
    """ReLU activation: h = max(0, z)"""
    
    def __init__(self):
        self.z = None  # Cache for backward
    
    def forward(self, z):
        self.z = z
        return np.maximum(0, z)
    
    def backward(self, dh):
        """Gradient flows through where z > 0, blocked where z <= 0"""
        return dh * (self.z > 0)
    
    def update(self, lr):
        pass  # No parameters to update

print("ReLU layer: h = max(0, z)")
print("  forward(z)  -> stores z, returns h")
print("  backward(dh) -> returns dh * (z > 0)")

ReLU layer: h = max(0, z)
  forward(z)  -> stores z, returns h
  backward(dh) -> returns dh * (z > 0)

Softmax + Cross-Entropy Loss¶

We combine softmax and cross-entropy into one layer because their combined gradient is simple: $\frac{\partial L}{\partial z} = p - y$

class SoftmaxCrossEntropy:
    """Combined softmax + cross-entropy loss"""
    
    def __init__(self):
        self.p = None  # Probabilities
        self.y = None  # True labels
    
    def forward(self, z, y):
        """
        z: raw scores (batch × classes)
        y: one-hot labels (batch × classes)
        Returns: scalar loss
        """
        # Softmax (with numerical stability)
        exp_z = np.exp(z - np.max(z, axis=1, keepdims=True))
        self.p = exp_z / np.sum(exp_z, axis=1, keepdims=True)
        self.y = y
        
        # Cross-entropy loss
        loss = -np.sum(y * np.log(self.p + 1e-8)) / len(y)
        return loss
    
    def backward(self):
        """The beautiful simplification: gradient is just (p - y)"""
        return (self.p - self.y) / len(self.y)

print("SoftmaxCrossEntropy layer:")
print("  forward(z, y) -> returns loss")
print("  backward()    -> returns (p - y) / batch_size")

SoftmaxCrossEntropy layer:
  forward(z, y) -> returns loss
  backward()    -> returns (p - y) / batch_size

The Network Class¶

Now we can stack layers into a network. The key insight: forward and backward are just loops!

class Network:
    """A neural network as a stack of layers"""
    
    def __init__(self, layer_sizes):
        """
        layer_sizes: list like [25, 8, 2] for input -> hidden -> output
        """
        self.layers = []
        
        # Create layers: Linear -> ReLU -> Linear -> ReLU -> ... -> Linear
        for i in range(len(layer_sizes) - 1):
            self.layers.append(Linear(layer_sizes[i], layer_sizes[i + 1]))
            # Add ReLU after all but the last linear layer
            if i < len(layer_sizes) - 2:
                self.layers.append(ReLU())
        
        # Loss function (applied separately)
        self.loss_fn = SoftmaxCrossEntropy()
        
        print(f"Created network: {layer_sizes}")
        print(f"  Layers: {[type(l).__name__ for l in self.layers]}")
    
    def forward(self, x):
        """Forward pass through all layers"""
        for layer in self.layers:
            x = layer.forward(x)
        return x
    
    def backward(self):
        """Backward pass through all layers (in reverse)"""
        grad = self.loss_fn.backward()
        for layer in reversed(self.layers):
            grad = layer.backward(grad)
    
    def update(self, lr):
        """Update all layer weights"""
        for layer in self.layers:
            layer.update(lr)
    
    def train_step(self, x, y, lr):
        """One complete training step"""
        # Forward
        z = self.forward(x)
        loss = self.loss_fn.forward(z, y)
        
        # Backward
        self.backward()
        
        # Update
        self.update(lr)
        
        return loss

# Example: create a 3-layer network
net = Network([25, 16, 8, 2])

Created network: [25, 16, 8, 2]
  Layers: ['Linear', 'ReLU', 'Linear', 'ReLU', 'Linear']

How It Works¶

The forward and backward passes are now just loops:

Forward:  x → [Linear → ReLU → Linear → ReLU → Linear] → z → Loss
             layer[0] layer[1] layer[2] layer[3] layer[4]

Backward: Loss → [Linear ← ReLU ← Linear ← ReLU ← Linear] ← gradient
                 layer[4] layer[3] layer[2] layer[1] layer[0]

Each layer:

Caches what it needs during forward
Uses that cache to compute gradients during backward
Returns the gradient for the layer below

Testing: Edge Detection with Flexible Architecture¶

Let’s verify our flexible network works by training it on the same edge detection task.

# Create training data (same as before)
def make_data(n_samples=100):
    X, y = [], []
    for _ in range(n_samples):
        if np.random.rand() > 0.5:
            # Edge: dark on left, bright on right
            edge_pos = np.random.randint(1, 4)
            patch = np.ones((5, 5)) * 0.1
            patch[:, edge_pos:] = 0.9
            label = [1, 0]
        else:
            # No edge
            if np.random.rand() > 0.5:
                patch = np.ones((5, 5)) * np.random.uniform(0.3, 0.7)
            else:
                patch = np.ones((5, 5)) * 0.9
                patch[:, 2:] = 0.1
            label = [0, 1]
        X.append(patch.flatten())
        y.append(label)
    return np.array(X), np.array(y)

X_train, y_train = make_data(200)
X_test, y_test = make_data(50)
print(f"Training: {len(X_train)} samples, Test: {len(X_test)} samples")

Training: 200 samples, Test: 50 samples

# Train with our flexible network!
# Try different architectures:

architectures = [
    [25, 2],           # No hidden layers (like logistic regression)
    [25, 8, 2],        # 1 hidden layer (like our original)
    [25, 16, 8, 2],    # 2 hidden layers
]

fig, axes = plt.subplots(1, 3, figsize=(15, 4))

for idx, arch in enumerate(architectures):
    np.random.seed(42)  # Same initialization for fair comparison
    
    net = Network(arch)
    losses = []
    
    # Training loop
    for epoch in range(200):
        # Mini-batch training
        epoch_loss = 0
        for i in range(0, len(X_train), 16):  # batch size 16
            batch_x = X_train[i:i+16]
            batch_y = y_train[i:i+16]
            loss = net.train_step(batch_x, batch_y, lr=0.1)
            epoch_loss += loss
        losses.append(epoch_loss / (len(X_train) / 16))
    
    # Evaluate
    z = net.forward(X_test)
    pred = np.argmax(z, axis=1)
    true = np.argmax(y_test, axis=1)
    accuracy = np.mean(pred == true) * 100
    
    # Plot
    axes[idx].plot(losses)
    axes[idx].set_xlabel('Epoch')
    axes[idx].set_ylabel('Loss')
    axes[idx].set_title(f'{arch}\nAccuracy: {accuracy:.1f}%')

plt.suptitle('Comparing Architectures on Edge Detection', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.show()

Created network: [25, 2]
  Layers: ['Linear']

Created network: [25, 8, 2]
  Layers: ['Linear', 'ReLU', 'Linear']

Created network: [25, 16, 8, 2]
  Layers: ['Linear', 'ReLU', 'Linear', 'ReLU', 'Linear']

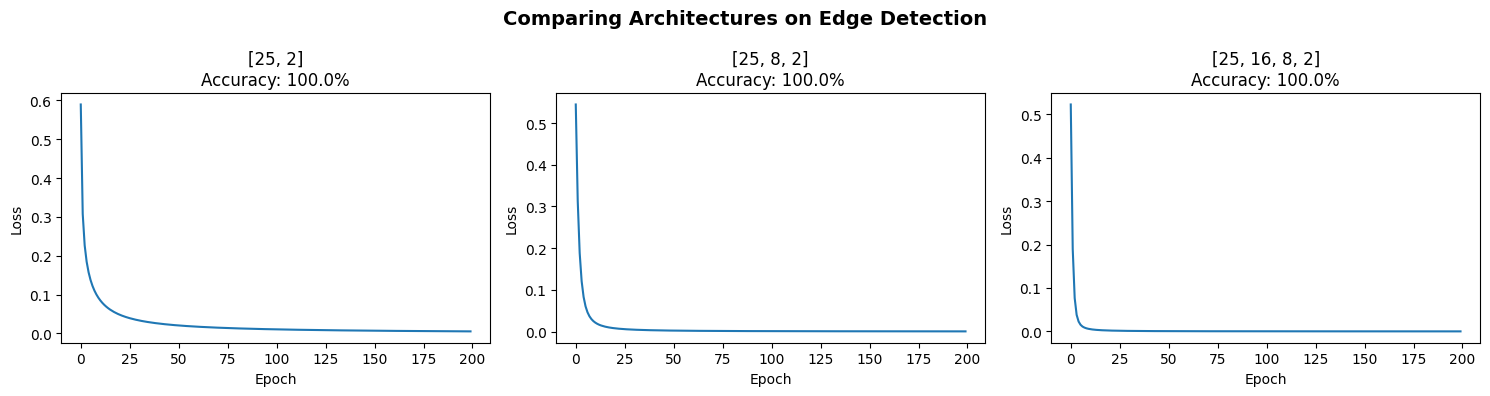
The Power of Flexibility¶

Now changing architectures is trivial:

# Shallow and wide
net = Network([784, 512, 10])

# Deep and narrow  
net = Network([784, 128, 64, 32, 10])

# Our edge detector
net = Network([25, 8, 2])

The same training code works for all of them!

Next: The PyTorch version¶

This NumPy implementation is the conceptual foundation. Next, we’ll rebuild the exact same flexible network using PyTorch modules and training loops, then use that as the base for CNNs, RNNs, and LSTMs.

Complete Code¶

Here’s the full implementation in ~100 lines:

"""
Flexible Neural Network from Scratch
=====================================
A minimal, clean implementation using only NumPy.
Supports arbitrary layer sizes like [784, 128, 64, 10].
"""

import numpy as np

# ============================================================
# LAYER CLASSES
# ============================================================

class Linear:
    """Fully connected layer: z = x @ W + b"""
    def __init__(self, in_features, out_features):
        self.W = np.random.randn(in_features, out_features) * np.sqrt(2.0 / in_features)
        self.b = np.zeros((1, out_features))
        self.x = None
        self.dW, self.db = None, None
    
    def forward(self, x):
        self.x = x
        return x @ self.W + self.b
    
    def backward(self, dz):
        self.dW = self.x.T @ dz
        self.db = np.sum(dz, axis=0, keepdims=True)
        return dz @ self.W.T
    
    def update(self, lr):
        self.W -= lr * self.dW
        self.b -= lr * self.db


class ReLU:
    """ReLU activation: h = max(0, z)"""
    def __init__(self):
        self.z = None
    
    def forward(self, z):
        self.z = z
        return np.maximum(0, z)
    
    def backward(self, dh):
        return dh * (self.z > 0)
    
    def update(self, lr):
        pass


class SoftmaxCrossEntropy:
    """Combined softmax + cross-entropy loss"""
    def __init__(self):
        self.p, self.y = None, None
    
    def forward(self, z, y):
        exp_z = np.exp(z - np.max(z, axis=1, keepdims=True))
        self.p = exp_z / np.sum(exp_z, axis=1, keepdims=True)
        self.y = y
        return -np.sum(y * np.log(self.p + 1e-8)) / len(y)
    
    def backward(self):
        return (self.p - self.y) / len(self.y)


# ============================================================
# NETWORK CLASS
# ============================================================

class Network:
    """A neural network as a stack of layers"""
    def __init__(self, layer_sizes):
        self.layers = []
        for i in range(len(layer_sizes) - 1):
            self.layers.append(Linear(layer_sizes[i], layer_sizes[i + 1]))
            if i < len(layer_sizes) - 2:
                self.layers.append(ReLU())
        self.loss_fn = SoftmaxCrossEntropy()
    
    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x
    
    def backward(self):
        grad = self.loss_fn.backward()
        for layer in reversed(self.layers):
            grad = layer.backward(grad)
    
    def update(self, lr):
        for layer in self.layers:
            layer.update(lr)
    
    def train_step(self, x, y, lr):
        z = self.forward(x)
        loss = self.loss_fn.forward(z, y)
        self.backward()
        self.update(lr)
        return loss


# ============================================================
# USAGE EXAMPLE
# ============================================================

if __name__ == "__main__":
    # Create network with any architecture
    net = Network([25, 16, 8, 2])
    
    # Generate dummy data
    X = np.random.randn(100, 25)
    y = np.eye(2)[np.random.randint(0, 2, 100)]
    
    # Train
    for epoch in range(100):
        loss = net.train_step(X, y, lr=0.01)
        if epoch % 20 == 0:
            print(f"Epoch {epoch}: Loss = {loss:.4f}")
    
    print("\nDone! Change [25, 16, 8, 2] to any architecture you want.")

Epoch 0: Loss = 0.8954
Epoch 20: Loss = 0.7847
Epoch 40: Loss = 0.7394
Epoch 60: Loss = 0.7117
Epoch 80: Loss = 0.6915

Done! Change [25, 16, 8, 2] to any architecture you want.

Summary¶

Key insights:

Layers are objects — each stores its weights and handles forward/backward
Forward pass is a loop — pass data through each layer in order
Backward pass is a reversed loop — pass gradients through each layer in reverse
Each layer caches what it needs — the input (for computing weight gradients)

The pattern for any layer:

def forward(self, x):
    self.cache = x          # Store what we need for backward
    return f(x)             # Compute output

def backward(self, grad_output):
    grad_weights = ...      # Use cache to compute weight gradients
    grad_input = ...        # Compute gradient for layer below
    return grad_input

What we gained:

Change architecture with one line: Network([784, 256, 128, 64, 10])
Same training code works for any depth
Easy to add new layer types (Dropout, BatchNorm, etc.)

Further Reading:

NN02 - Training an Edge-Detection Neural Network from Scratch — The concepts behind this code
PyTorch nn.Module — How the pros do it (same pattern!)