Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

How neural networks turn raw scores into probabilities for classification

This post is a standalone explanation of softmax that you can reference from any classifier walkthrough, whether it is an image model, a text model, or a simple toy example.

Where Does Softmax Fit?

Before diving into how softmax works, let’s see where it sits in a classification pipeline. Here’s a simple edge detection network:

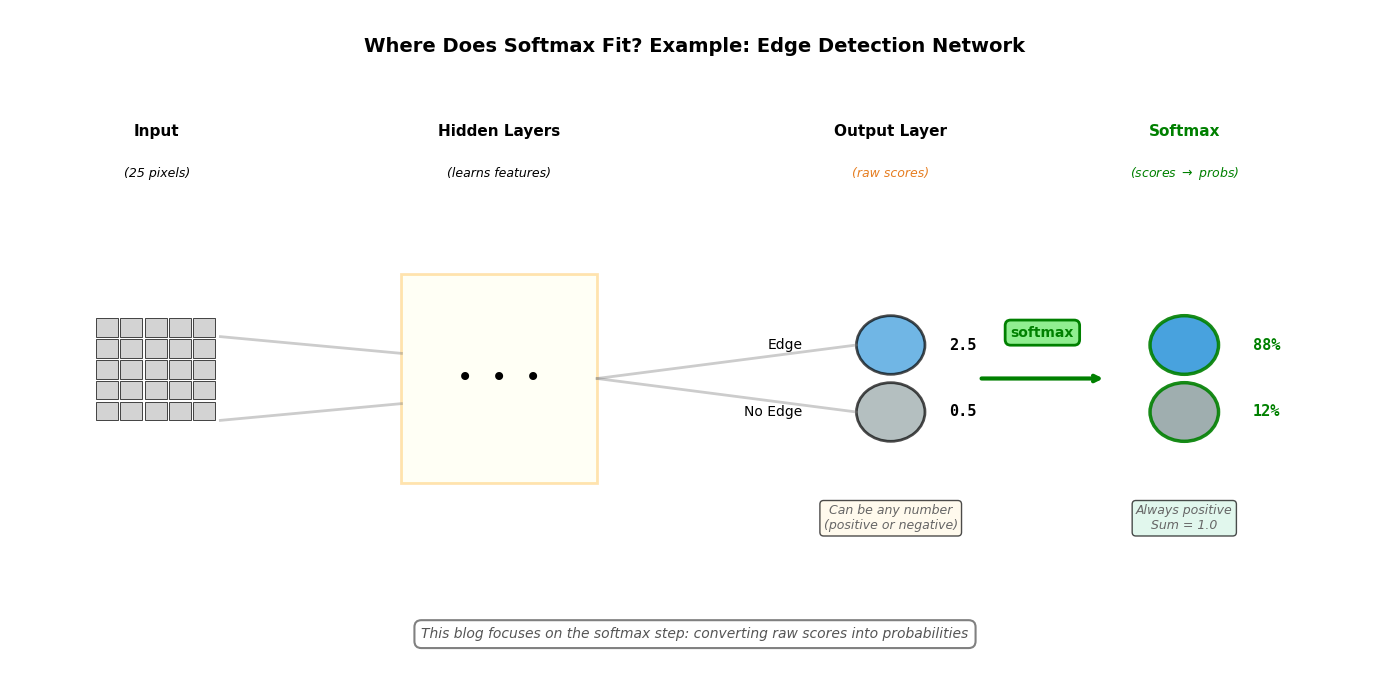
<Figure size 1400x700 with 1 Axes>

The key point: Softmax operates on the final layer’s raw scores, converting them into probabilities that sum to 1. The rest of this post explains how softmax works, regardless of the network architecture.

From Scores to Probabilities - Softmax

In a classification model, the final layer produces scores (also called logits) — higher means the model favors that class more. But for classification, we need probabilities: “What’s the chance this is an edge?”

Suppose our model has two output neurons (one for “Edge”, one for “No Edge”), each producing a score. So we have a vector of scores z=[zedge,zno_edge]\mathbf{z} = [z_{edge}, z_{no\_edge}]. These raw scores can be any number — positive, negative, or zero.

📘 Terminology: Logits

The raw scores before softmax are called logits. You’ll see this term everywhere in machine learning.

  • Logits can be any real number (−∞ to +∞)

  • Softmax converts logits → probabilities (0 to 1, summing to 1)

Softmax converts this score vector into a probability vector where:

  1. All values are positive

  2. They sum to 1.0

The Intuition: It’s Just a Ratio

At its core, softmax answers: “What fraction of the total is each score?”

If we only had positive scores, we could just divide by the sum:

pj=zj∑kzkp_j = \frac{z_j}{\sum_k z_k}
(1)

Where:

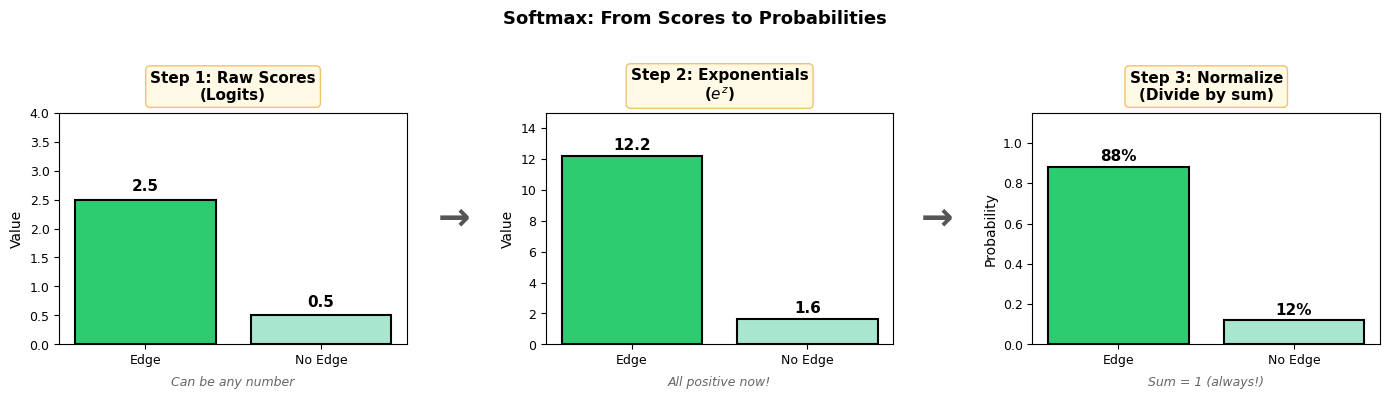
For example, scores [3,1][3, 1] would give p0=3/(3+1)=0.75p_0 = 3/(3+1) = 0.75 and p1=1/(3+1)=0.25p_1 = 1/(3+1) = 0.25.

The problem: Scores can be negative or zero, which breaks this.

The solution: First apply eze^z to make everything positive, then take the ratio.

The Formula

pj=ezj∑kezkp_j = \frac{e^{z_j}}{\sum_{k} e^{z_k}}
(2)

The exponential also amplifies differences — a score of 5 vs 3 becomes e5e^5 vs e3e^3 (148 vs 20), making the network more confident.

The visualization below shows the 3-step process:

<Figure size 1400x400 with 3 Axes>

Implementation:

# z is a vector of scores (logits) for all classes
z = np.array([2.5, 0.5])            # e.g., [Edge score, No-Edge score]

exp_z = np.exp(z)                   # exponentiate each element
p = exp_z / np.sum(exp_z)           # normalize → probability vector

print(f"Logits z: {z}")             # [2.5, 0.5]
print(f"exp(z):   {exp_z}")         # [12.18, 1.65]
print(f"Probs p:  {p}")             # [0.88, 0.12]

This computes all pjp_j values at once: p[j] = ezj∑kezk\frac{e^{z_j}}{\sum_k e^{z_k}}

Note on Numerical Stability: In practice, we subtract the max score before exponentiating to prevent overflow. This is safe because the constants cancel in the ratio:

ezj−c∑kezk−c=ezj/ec∑k(ezk/ec)=ezj∑kezk\frac{e^{z_j - c}}{\sum_k e^{z_k - c}} = \frac{e^{z_j}/e^{c}}{\sum_k (e^{z_k}/e^{c})} = \frac{e^{z_j}}{\sum_k e^{z_k}}
(3)

So we can choose c=max⁡(z)c = \max(z) without changing the result:

exp_z = np.exp(z - np.max(z))        # stable: prevents overflow
p = exp_z / np.sum(exp_z)            # same result as before

Multi-Class Example

Softmax works for any number of classes, not just two. Here’s a 3-class example:

# Multi-class classification: Cat, Dog, Bird
z = np.array([3.2, 1.3, 0.2])           # scores for each class

exp_z = np.exp(z - np.max(z))           # stable computation
p = exp_z / np.sum(exp_z)               # normalize

print(f"Logits:  {z}")                  # [3.2, 1.3, 0.2]
print(f"Probs:   {p}")                  # [0.70, 0.24, 0.06]
print(f"Sum:     {p.sum():.1f}")        # 1.0

# Interpretation: 70% Cat, 24% Dog, 6% Bird

The highest score (3.2 for Cat) gets the highest probability (70%), but the other classes still have non-zero probabilities. This is useful for understanding model confidence and handling uncertain predictions.

Common Pitfalls

⚠️ Things to Watch Out For

1. Don’t apply softmax to already-normalized outputs

  • If your network already outputs probabilities (sum to 1), softmax is redundant

  • Example: Don’t apply softmax after another softmax layer

2. Softmax is for classification, not regression

  • Use softmax when predicting categories (cat, dog, bird)

  • Don’t use it for continuous values (e.g., predicting temperature or price)

  • For regression, use raw outputs or other activation functions

3. Softmax is differentiable

  • This is crucial for training neural networks with backpropagation

  • The gradient flows through softmax during training

  • You typically use cross-entropy loss with softmax for classification

4. Temperature scaling

  • Dividing logits by temperature T before softmax affects confidence:

    • T > 1: Less confident, more uniform probabilities

    • T < 1: More confident, sharper probabilities

    • Default T = 1 (standard softmax)

Summary

Softmax converts raw scores (logits) into probabilities:

Key formula: pj=ezj∑kezkp_j = \frac{e^{z_j}}{\sum_k e^{z_k}}

This makes softmax the standard final layer activation for multi-class classification in neural networks.

ML/AI Algorithms
Alternating Least Squares (ALS) for Movie Recommendations
ML/AI Algorithms
Tree-Based Feature Importance [DRAFT]