L04 - Multi-Head Attention: The Committee of Experts

Why one brain is good, but eight brains are better.

In L03 - Self-Attention, we built the “Search Engine” of the Transformer. We learned how the word “it” can look up the word “animal” to resolve ambiguity.

But there is a limitation. A single self-attention layer acts like a single pair of eyes. It can focus on one aspect of the sentence at a time.

Consider the sentence:

“The chicken didn’t cross the road because it was too wide.”

To understand this fully, the model needs to do two things simultaneously:

Syntactic Analysis: Link “it” to the subject “road” (because roads are wide).
Semantic Analysis: Understand that “wide” is a physical property preventing crossing.

If we only have one attention head, the model has to average these different relationships into a single vector. It muddies the waters.

Multi-Head Attention solves this by giving the model multiple “heads” (independent attention mechanisms) that run in parallel.

By the end of this post, you’ll understand:

The intuition of the “Committee of Experts.”
Why we project vectors into different Subspaces.
How to implement the tensor reshaping magic (view and transpose) in PyTorch.

import os
import logging
import warnings

logging.getLogger("matplotlib.font_manager").setLevel(logging.ERROR)
warnings.filterwarnings("ignore", message="Matplotlib is building the font cache*")

import torch
import torch.nn as nn
import matplotlib
import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['figure.facecolor'] = 'white'
plt.rcParams['axes.facecolor'] = 'white'

Part 1: The Intuition (The Committee)¶

Think of the embedding dimension ( $d_{model} = 512$ ) as a massive report containing everything we know about a word.

If we ask a single person to read that report and summarize “grammar,” “tone,” “tense,” and “meaning” all at once, they might miss details.

Instead, we hire a Committee of 8 Experts:

Head 1 (The Linguist): Only looks for Subject-Verb agreement.
Head 2 (The Historian): Looks for past/present tense consistency.
Head 3 (The Translator): Looks for definitions and synonyms.
...

In the Transformer, we don’t just copy the input 8 times. We project the input into 8 different lower-dimensional spaces. This allows each head to specialize.

Let’s visualize this “filtering” process. In the plot below:

The Input (Mixed Info): The large multi-colored bar represents the full word embedding ( $d=512$ ).
The Split (Equal Parts): We project this into 8 equal-sized subspaces ( $d_k = 64$ ).
The Result: Each head gets a vector that is 1/8th the size of the original, containing only the specific info it needs.

import matplotlib.pyplot as plt
import matplotlib.patches as patches
import numpy as np

def plot_multihead_projection_concept():
    fig, ax = plt.subplots(figsize=(14, 8)) # Increased size slightly
    ax.set_xlim(0, 14)
    ax.set_ylim(0, 9)
    ax.axis('off')

    # --- Configuration ---
    input_x = 1
    output_x = 10
    
    # Coordinates for the "Heads" (Outputs)
    # We show them essentially "stacking up" to equal the total concept, 
    # but separated to show independence.
    y_positions = [7, 4.5, 2] 
    colors = ['#FF9999', '#99FF99', '#9999FF'] 
    labels = ["Head 1\nGrammar", "Head 2\nTense", "Head 3\nMeaning"]

    # FONT SIZES
    font_title = 20
    font_label = 16
    font_math = 14
    font_annot = 14

    # --- 1. Draw Input Vector (The "General Report") ---
    height = 6
    width = 1.5
    base_y = 1.5
    
    # Container
    input_rect = patches.Rectangle((input_x, base_y), width, height, linewidth=3, edgecolor='black', facecolor='none', zorder=5)
    ax.add_patch(input_rect)
    
    # "Mixed Info" bands
    num_segments = 20
    seg_height = height / num_segments
    np.random.seed(42) 
    segment_colors = plt.get_cmap('tab20').colors
    for i in range(num_segments):
        color = segment_colors[i % len(segment_colors)]
        rect = patches.Rectangle((input_x, base_y + i*seg_height), width, seg_height, facecolor=color, alpha=0.7, edgecolor='none')
        ax.add_patch(rect)

    # Label Input
    ax.text(input_x + width/2, base_y - 0.6, "Input Embedding\n($d_{model}=512$)", ha='center', va='top', fontweight='bold', fontsize=font_label)

    # --- 2. Draw The Projections (Arrows & Matrices) ---
    
    proj_start_x = input_x + width + 0.2
    proj_end_x = output_x - 0.2
    
    for i, (y_c, color, label) in enumerate(zip(y_positions, colors, labels)):
        # A. Arrow from Input Center to Head Center
        arrow = patches.FancyArrowPatch(
            (proj_start_x, base_y + height/2), (proj_end_x, y_c),
            arrowstyle='-|>,head_width=0.6,head_length=1.0',
            connectionstyle=f"arc3,rad={(i-1)*-0.15}", 
            color=color, lw=4, zorder=2, alpha=0.8
        )
        ax.add_patch(arrow)
        
        # B. Matrix Box (The "Lens")
        mid_x = (proj_start_x + proj_end_x) / 2
        mid_y = (base_y + height/2 + y_c) / 2 + (i-1)*0.5 # Slight offset for visual separation
        
        # Matrix Label
        ax.text(mid_x, mid_y + 0.6, f"$W_{i}$", ha='center', va='center', color=color, fontweight='bold', fontsize=font_label, zorder=6)

        # C. Output Subspace Blocks
        # Make them look identical in size
        out_h = 1.8
        out_w = 1.5
        out_rect = patches.Rectangle((output_x, y_c - out_h/2), out_w, out_h, facecolor=color, edgecolor='black', lw=2, alpha=0.9)
        ax.add_patch(out_rect)
        
        # Label each head
        ax.text(output_x + out_w + 0.3, y_c, label, ha='left', va='center', fontsize=font_label, color='black')
        # Math label showing the split
        ax.text(output_x + out_w + 0.3, y_c - 0.6, "($d_k=64$)", ha='left', va='center', fontsize=font_math, color='#555')

    # --- 3. Final Annotations describing the Split ---
    
    # Title
    ax.text(7, 8.5, "Multi-Head Projection: Dividing the Work", ha='center', va='center', fontsize=font_title, fontweight='bold')
    
    # Explanation of the split
    ax.text(7, 0.5, "Total Dimensions (512) $\\div$ Heads (8) = 64 dims per Head", 
            ha='center', va='center', fontsize=font_label, fontweight='bold', 
            bbox=dict(facecolor='#f0f0f0', edgecolor='gray', boxstyle='round,pad=0.5'))

    plt.tight_layout()
    plt.show()

plot_multihead_projection_concept()

Technical Note: What actually gets split?

You might look at the diagram and wonder: “Does Head 1 just look at the first 64 numbers of the input?”

No. That would be disastrous, because the first 64 numbers of the embedding might not contain the specific grammar information Head 1 needs.

The process happens in two specific steps:

The Mix (Linear Layer): First, the input vector (512) is multiplied by the weight matrix ( $W$ ). This operation has access to the entire input vector. It blends all the information together.
The Split (Reshape): The result of that multiplication is a new 512-dimensional vector. This new vector is what gets chopped into 8 chunks of 64.

So, Head 1 can see the whole input, but the Linear Layer ensures that the information Head 1 needs ends up in the “first chunk” (indices 0-63) of the output.

Part 2: The Multi-Head Pipeline¶

Now that we understand the “why” (Specialization), let’s look at the “how” (The Pipeline).

The Multi-Head Attention mechanism isn’t a single black box; it is a specific sequence of operations. It allows the model to process information in parallel and then synthesize the results.

The 4-Step Process

Linear Projections (The Split): We don’t just use the raw input. We multiply the input $Q, K, V$ by specific weight matrices ( $W^Q_i, W^K_i, W^V_i$ ) for each head. This creates the specialized “subspaces” we saw in Part 1.
Independent Attention: Each head runs the standard Scaled Dot-Product Attention independently.
$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$
(1)
Concatenation: We take the output vectors from all 8 heads and glue them back together side-by-side.
Final Linear (The Mix): We pass this long concatenated vector through one last linear layer ( $W^O$ ) to blend the insights from all the experts into a single unified vector.

\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O

(2)

Let’s visualize this flow:

Part 3: Visualizing Multiple Perspectives¶

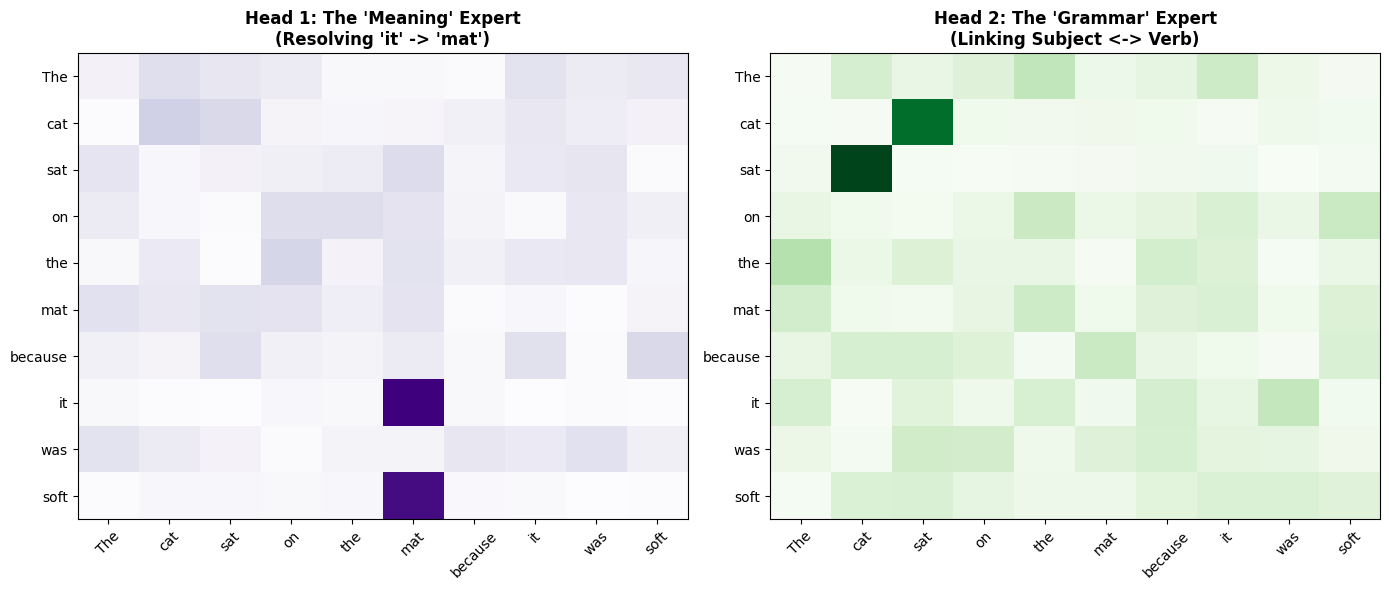
Let’s visualize how two different heads might analyze the same sentence.

Sentence: “The cat sat on the mat because it was soft.”

Head 1 focuses on the physical relationship (connecting “it” to “mat”).
Head 2 focuses on the actor (connecting “sat” to “cat”).

Notice how they highlight completely different parts of the matrix.

tokens = ["The", "cat", "sat", "on", "the", "mat", "because", "it", "was", "soft"]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Head 1: Reference Resolution (it -> mat)
# Simulating a head that understands physical properties
head1 = np.zeros((len(tokens), len(tokens)))
head1[tokens.index("it"), tokens.index("mat")] = 0.95
head1[tokens.index("soft"), tokens.index("mat")] = 0.8
# Add some background noise
np.random.seed(42)
head1 += np.random.rand(len(tokens), len(tokens)) * 0.05
# Normalize
head1 = head1 / head1.sum(axis=1, keepdims=True)

# Head 2: Syntax / Subject-Verb (sat -> cat)
# Simulating a head that connects verbs to their subjects
head2 = np.zeros((len(tokens), len(tokens)))
head2[tokens.index("cat"), tokens.index("sat")] = 0.6
head2[tokens.index("sat"), tokens.index("cat")] = 0.9
head2 += np.random.rand(len(tokens), len(tokens)) * 0.05
head2 = head2 / head2.sum(axis=1, keepdims=True)

# Plotting Head 1
im1 = ax1.imshow(head1, cmap='Purples', aspect='auto')
ax1.set_title("Head 1: The 'Meaning' Expert\n(Resolving 'it' -> 'mat')", fontsize=12, fontweight='bold')
ax1.set_xticks(range(len(tokens)))
ax1.set_xticklabels(tokens, rotation=45)
ax1.set_yticks(range(len(tokens)))
ax1.set_yticklabels(tokens)
ax1.grid(False)

# Plotting Head 2
im2 = ax2.imshow(head2, cmap='Greens', aspect='auto')
ax2.set_title("Head 2: The 'Grammar' Expert\n(Linking Subject <-> Verb)", fontsize=12, fontweight='bold')
ax2.set_xticks(range(len(tokens)))
ax2.set_xticklabels(tokens, rotation=45)
ax2.set_yticks(range(len(tokens)))
ax2.set_yticklabels(tokens)
ax2.grid(False)

plt.tight_layout()
plt.show()

Part 4: Implementation in PyTorch¶

Implementing this efficiently requires some tensor gymnastics. We don’t actually run a for loop over the 8 heads. That would be too slow.

Instead, we use a single large matrix multiply and then reshape (view/transpose) the tensor to create a “heads” dimension.

The shape transformation looks like this:

Input: [Batch, Seq_Len, D_Model]
Linear & Reshape: [Batch, Seq_Len, Heads, D_Head]
Transpose: [Batch, Heads, Seq_Len, D_Head]

By swapping axes 1 and 2, we group the “Heads” dimension with the “Batch” dimension. PyTorch then processes all heads in parallel as if they were just extra items in the batch.

Shape Transformation Table¶

Let’s trace the exact tensor shapes through a concrete example with batch=2, seq=10, d_model=512, heads=8:

Operation	Shape	Description
Input `x`	`[2, 10, 512]`	Raw input: 2 sequences, each with 10 tokens, 512-dim embeddings
After `W_q(x)`	`[2, 10, 512]`	Linear projection (still flat)
After `.view(2, 10, 8, 64)`	`[2, 10, 8, 64]`	Reshape: Split 512 dims into 8 heads × 64 dims each
After `.transpose(1, 2)`	`[2, 8, 10, 64]`	Swap seq and heads: Now we have 8 “parallel attention mechanisms”
Attention computation	`[2, 8, 10, 64]`	Each head computes attention independently
After `.transpose(1, 2)`	`[2, 10, 8, 64]`	Swap back: Prepare for concatenation
After `.contiguous().view(2, 10, 512)`	`[2, 10, 512]`	Flatten: Merge 8 heads back into single 512-dim vector
After `W_o(x)`	`[2, 10, 512]`	Final projection

The key insight: dimensions 1 and 2 get swapped twice—once to parallelize the heads, and once to merge them back together.

import math
import torch
import torch.nn as nn
import torch.nn.functional as F

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super().__init__()
        assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
        
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_k = d_model // num_heads
        
        # We define 4 linear layers: Q, K, V projections and the final Output
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        self.W_o = nn.Linear(d_model, d_model)
        
    def forward(self, q, k, v, mask=None):
        batch_size = q.size(0)
        
        # 1. Project and Split
        # We transform [Batch, Seq, Model] -> [Batch, Seq, Heads, d_k]
        # Then we transpose to [Batch, Heads, Seq, d_k] for matrix multiplication
        Q = self.W_q(q).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        K = self.W_k(k).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        V = self.W_v(v).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        
        # 2. Scaled Dot-Product Attention (re-using logic from L03)
        # Scores shape: [Batch, Heads, Seq, Seq]
        scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
        
        if mask is not None:
            scores = scores.masked_fill(mask == 0, -1e9)
        
        attn_weights = torch.softmax(scores, dim=-1)
        
        # Apply weights to Values
        # Shape: [Batch, Heads, Seq, d_k]
        attn_output = torch.matmul(attn_weights, V)
        
        # 3. Concatenate
        # Transpose back: [Batch, Seq, Heads, d_k]
        # Flatten: [Batch, Seq, d_model]
        attn_output = attn_output.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)
        
        # 4. Final Projection (The "Mix")
        return self.W_o(attn_output)

Why .contiguous()? Understanding Memory Layout

When we transpose a tensor in PyTorch, we aren’t actually moving data in memory; we are just changing the “stride” (how the computer steps through memory).

Memory Layout Explanation:

Tensors are stored as 1D arrays in memory. Multi-dimensional tensors use “strides” to map from indices to memory locations.
When you call .transpose(), PyTorch creates a new view with different strides, but the underlying data stays in the same physical order in memory.
The view() operation requires the data to be laid out in a specific order in memory (row-major, also called C-contiguous).
If the tensor isn’t contiguous after transpose, calling .view() would give incorrect results or raise an error.

What .contiguous() does:

Creates a new tensor with data physically rearranged in memory to match the current logical shape.
This is a copy operation, so it has a performance cost, but it’s necessary to ensure correctness.

Example:

x = torch.randn(2, 3, 4)
x_t = x.transpose(1, 2)  # Creates a view, not contiguous
print(x_t.is_contiguous())  # False
x_c = x_t.contiguous()      # Creates a contiguous copy
print(x_c.is_contiguous())  # True

This is a PyTorch implementation detail; the math doesn’t care about memory layout, but the computer does!

Summary¶

Multiple Heads: We split our embedding into $h$ smaller chunks to allow the model to focus on different linguistic features simultaneously.
Projection: We use learned linear layers ( $W_Q, W_K, W_V$ ) to project the input into these specialized subspaces.
Parallelism: We use tensor reshaping (view and transpose) to compute attention for all heads at once, rather than looping through them.

Next Up: L05 – Layer Norm & Residuals. We have built the engine (Attention), but if we stack 100 of these layers on top of each other, the gradients will vanish or explode. In L05, we will add the “plumbing” (Normalization and Skip Connections) that allows Deep Learning to actually get deep.