L05 - Normalization & Residuals: The Plumbing of Deep Networks [DRAFT]

How to stop gradients from vanishing and signals from exploding

We have built the Multi-Head Attention engine, but there is a problem. In a deep LLM, we stack these layers dozens of times. As the data passes through these transformations, the numbers can drift: they might become tiny (vanishing) or massive (exploding).

If the numbers get weird, the model stops learning. To fix this, we use two critical “plumbing” techniques:

Residual (Skip) Connections: “Don’t forget what you just learned.”
Layer Normalization: “Keep the numbers in a healthy range.”

By the end of this post, you’ll understand:

The intuition behind Add & Norm.
Why Residual Connections allow for incredibly deep models.
How to implement LayerNorm from scratch.

import os
import logging
import warnings

logging.getLogger("matplotlib.font_manager").setLevel(logging.ERROR)
warnings.filterwarnings("ignore", message="Matplotlib is building the font cache*")

import torch
import torch.nn as nn
import matplotlib
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['figure.facecolor'] = 'white'
plt.rcParams['axes.facecolor'] = 'white'

Part 1: Residual Connections (The Skip)¶

In a standard network, data flows like this: . In a Transformer, we do this: .

We literally add the input back to the output.

Why?

Imagine you are trying to describe a complex concept. If you only give the “transformed” explanation, you might lose the original context. By adding the input back, we provide a “highway” for the original signal to travel through.

The Gradient Flow Advantage

The real magic of residual connections becomes clear during backpropagation. Consider a deep network with 100 layers:

Without Residuals:

The gradient must flow through: Layer 100 → Layer 99 → ... → Layer 1
Each layer multiplies the gradient by its weight matrix derivatives
After 100 multiplications, the gradient often becomes vanishingly small (gradient vanishing) or explodes

With Residuals: $y = x + F(x)$

The derivative is: $\frac{dy}{dx} = 1 + \frac{dF}{dx}$
The “+1” term creates a direct path for gradients to flow backward
Even if $\frac{dF}{dx}$ is tiny, the gradient still has magnitude ~1 from the identity path
This allows training of networks with 100+ layers successfully

Analogy: It’s like having both local roads (the transformation layers) and a highway (the skip connection). If local roads get congested, traffic can still flow via the highway.

This is why ResNets, Transformers, and other modern architectures can be so deep—residual connections solved the vanishing gradient problem that plagued earlier deep networks.

Visualizing Gradient Flow: With vs. Without Residuals¶

Let’s see the dramatic difference residual connections make in a deep network:

import numpy as np
import matplotlib.pyplot as plt

# Simulate gradient magnitudes through layers
num_layers = 20
layers = np.arange(1, num_layers + 1)

# Without residuals: exponential decay (vanishing gradients)
# Each layer multiplies gradient by ~0.8 (typical for deep networks)
gradient_without_residual = np.power(0.8, layers - 1)

# With residuals: gradient stays stable due to identity path
# The "+1" term in the derivative prevents vanishing
gradient_with_residual = 0.7 + 0.3 * np.power(0.9, layers - 1)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# Plot 1: Gradient Magnitude
ax1.plot(layers, gradient_without_residual, 'o-', label='Without Residuals',
         color='red', linewidth=2, markersize=6)
ax1.plot(layers, gradient_with_residual, 's-', label='With Residuals',
         color='green', linewidth=2, markersize=6)
ax1.axhline(y=0.1, color='gray', linestyle='--', alpha=0.5, label='Vanishing Threshold')
ax1.set_xlabel('Layer Depth', fontsize=12)
ax1.set_ylabel('Gradient Magnitude', fontsize=12)
ax1.set_title('Gradient Flow Through Deep Network', fontsize=14, fontweight='bold')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax1.set_yscale('log')

# Plot 2: Layer-by-layer comparison
bar_width = 0.35
x_pos = np.arange(len(layers[:10]))
ax2.bar(x_pos - bar_width/2, gradient_without_residual[:10], bar_width,
        label='Without Residuals', color='red', alpha=0.7)
ax2.bar(x_pos + bar_width/2, gradient_with_residual[:10], bar_width,
        label='With Residuals', color='green', alpha=0.7)
ax2.set_xlabel('Layer Number', fontsize=12)
ax2.set_ylabel('Gradient Magnitude', fontsize=12)
ax2.set_title('First 10 Layers (Zoomed)', fontsize=14, fontweight='bold')
ax2.set_xticks(x_pos)
ax2.set_xticklabels(layers[:10])
ax2.legend()
ax2.grid(True, alpha=0.3, axis='y')

plt.tight_layout()
plt.show()

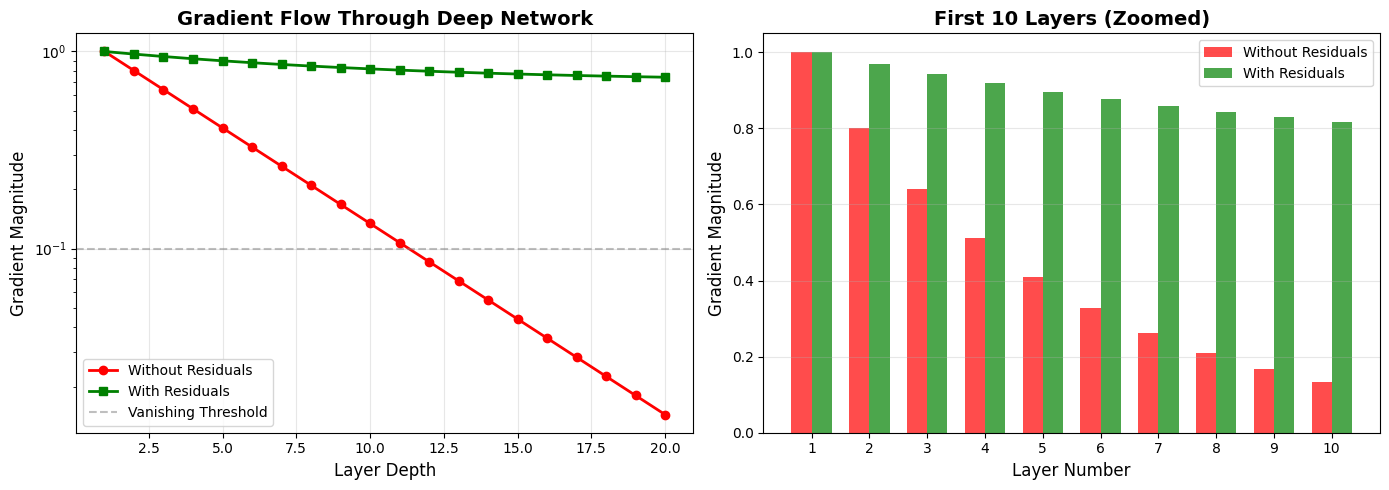
Key observations:

Without residuals (red): Gradients decay exponentially, reaching near-zero by layer 10-15
With residuals (green): Gradients remain strong even in deep layers
This is why we can train 100+ layer transformers successfully!

Part 2: Layer Normalization (The Leveler)¶

LayerNorm ensures that for every token, the mean of its features is 0 and the standard deviation is 1. This prevents any single feature or layer from dominating the calculation.

Unlike BatchNorm (common in CNNs), LayerNorm calculates statistics across the features of a single token. This makes it perfect for sequences of varying lengths.

LayerNorm vs. BatchNorm: What’s the Difference?¶

Both normalization techniques aim to stabilize training, but they compute statistics over different dimensions:

Aspect	BatchNorm	LayerNorm
Normalizes across	Batch dimension (across examples)	Feature dimension (within each example)
Input shape	`[Batch, Features]` or `[Batch, Channels, Height, Width]`	`[Batch, Seq_Len, Features]`
Statistics computed	Mean/Std for each feature across all examples in batch	Mean/Std for each example across all features
Dependencies	Requires large batches to get good statistics	Works with batch size = 1
Typical use	CNNs (image tasks)	Transformers, RNNs (sequence tasks)

Why LayerNorm for Transformers?

Variable sequence lengths: Different sentences have different lengths. BatchNorm would struggle with varying dimensions.
Batch independence: Each example can be normalized independently, making it work even with tiny batches (e.g., batch_size=1 during inference).
Recurrent/sequential nature: In sequences, we care about the distribution of features within each token, not across different tokens in a batch.

Visual Comparison:

BatchNorm (shape [4, 512]):          LayerNorm (shape [4, 512]):
┌─────────────────┐                  ┌─────────────────┐
│ Example 1       │                  │ Example 1       │ ← Normalize these 512 values
│ Example 2       │ ↑                │ Example 2       │ ← Normalize these 512 values
│ Example 3       │ │ Normalize      │ Example 3       │ ← Normalize these 512 values
│ Example 4       │ │ each column    │ Example 4       │ ← Normalize these 512 values
└─────────────────┘ ↓                └─────────────────┘

The Formula

For a vector :

\hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \cdot \gamma + \beta

(1)

Calculate mean () and variance () of the features.
Subtract mean and divide by standard deviation.
Learnable Parameters: (scale) and (shift) allow the model to “undo” the normalization if it decides that a different range is better for learning.

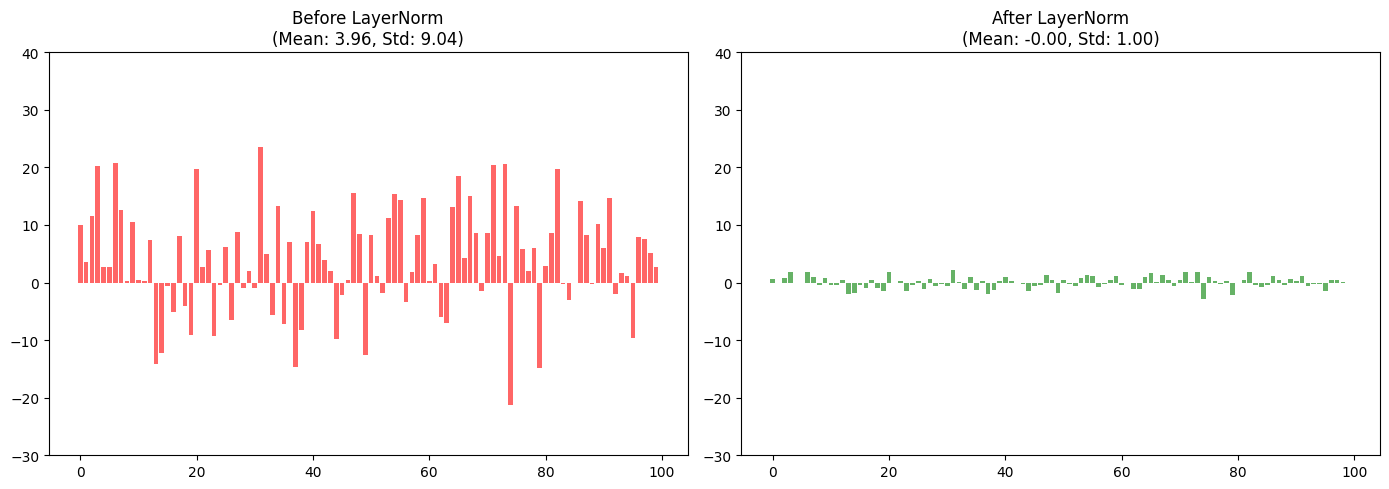
Part 3: Visualizing the “Add & Norm”¶

Let’s see how LayerNorm tames wild values.

# Create a "wild" vector of 100 features
np.random.seed(42)
wild_vector = np.random.normal(loc=5, scale=10, size=100)

# Normalize manually
mean = wild_vector.mean()
std = wild_vector.std()
norm_vector = (wild_vector - mean) / std

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

ax1.bar(range(100), wild_vector, color='red', alpha=0.6)
ax1.set_title(f"Before LayerNorm\n(Mean: {mean:.2f}, Std: {std:.2f})")
ax1.set_ylim(-30, 40)

ax2.bar(range(100), norm_vector, color='green', alpha=0.6)
ax2.set_title(f"After LayerNorm\n(Mean: {norm_vector.mean():.2f}, Std: {norm_vector.std():.2f})")
ax2.set_ylim(-30, 40)

plt.tight_layout()
plt.show()

Part 4: Building LayerNorm from Scratch¶

While PyTorch has nn.LayerNorm, building it yourself helps you understand exactly where those learnable parameters () live.

class LayerNorm(nn.Module):
    def __init__(self, d_model, eps=1e-6):
        super().__init__()
        self.gamma = nn.Parameter(torch.ones(d_model))
        self.beta = nn.Parameter(torch.zeros(d_model))
        self.eps = eps

    def forward(self, x):
        # x shape: [batch, seq_len, d_model]
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        
        # Normalize
        x_norm = (x - mean) / (std + self.eps)
        
        # Scale and Shift
        return self.gamma * x_norm + self.beta

Part 5: Pre-Norm vs. Post-Norm - Where to Place LayerNorm?¶

There are two ways to combine residuals and normalization in a Transformer block, and the choice has significant training implications:

Post-Norm (Original Transformer)¶

x = LayerNorm(x + Attention(x))
x = LayerNorm(x + FeedForward(x))

How it works:

Apply the transformation (Attention or FFN)
Add the residual
Normalize the result

Characteristics:

Used in the original “Attention is All You Need” paper
Gradients can still be large early in training
Often requires learning rate warmup and careful tuning

Pre-Norm (Modern Standard)¶

x = x + Attention(LayerNorm(x))
x = x + FeedForward(LayerNorm(x))

How it works:

Normalize the input first
Apply the transformation
Add the residual

Characteristics:

Used by GPT-2, GPT-3, and most modern LLMs
More stable gradients throughout training
Easier to train (less sensitive to hyperparameters)
The residual path stays “clean” (unnormalized)

Visual Comparison¶

Post-Norm Architecture

Pre-Norm Architecture

Why Pre-Norm Won:

Empirically, Pre-Norm is more stable and easier to optimize
The gradient flowing through the residual connection doesn’t pass through LayerNorm
Works better for very deep networks (100+ layers)

Summary¶

Residual Connections create a “high-speed rail” for the signal, preventing the vanishing gradient problem through the “+1” term in gradients.
LayerNorm re-centers the data at every step, keeping the optimization process stable by normalizing across features rather than across batches.
Pre-Norm vs. Post-Norm: Most modern LLMs use Pre-Norm (normalize before the sub-layer) because it’s more stable to train and less sensitive to hyperparameters.

Next Up: L06 – The Causal Mask. When training a model to predict the next word, how do we stop it from “cheating” by looking at the answer? We’ll build the triangular mask that hides the future.