L06 - The Causal Mask: How to Stop Cheating [DRAFT]

The triangular trick that forces models to predict the future

In L03 - Self-Attention, we learned that every word looks at every other word. That’s fine for an “Encoder” (like BERT) that just wants to understand a sentence.

But a Generative LLM (like GPT) is a Decoder. Its only job is to look at the words so far and guess the next word. If we allow the token at position 2 to “attend” to the token at position 3 during training, the model will simply memorize the data rather than learning the patterns of language.

By the end of this post, you’ll understand:

The intuition of Causal Masking.
Why we use $-\infty$ (negative infinity) in our attention scores.
How to implement the Lower Triangular Mask from scratch.

import os
import logging
import warnings

logging.getLogger("matplotlib.font_manager").setLevel(logging.ERROR)
warnings.filterwarnings("ignore", message="Matplotlib is building the font cache*")

import torch
import matplotlib
import numpy as np

import matplotlib.pyplot as plt

plt.rcParams['figure.facecolor'] = 'white'
plt.rcParams['axes.facecolor'] = 'white'

Part 1: The Intuition (The “No Peeking” Rule)¶

Imagine you are taking a test where you have to finish a sentence. “The cat sat on the ___”

If the full sentence “The cat sat on the mat” is written on the back of the page and the paper is transparent, you’ll just look through the paper. Causal Masking is like putting a piece of cardboard over the words that haven’t been “written” yet.

Part 2: The Masking Math¶

Recall our attention score formula:

\text{Scores} = \frac{QK^T}{\sqrt{d_k}}

(1)

This produces a square matrix where every row represents a word, and every column represents how much it cares about word .

To “mask” the future, we want to make the scores for any effectively zero. But we don’t just set them to 0; we set them to .

Why a large negative number (like $-\infty$ or -10⁹)? Because we apply a Softmax immediately after.

\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}

(2)

When $x_i = -\infty$ , then $e^{-\infty} = 0$ . By setting the “future” scores to a very large negative number, the Softmax will assign them a probability of exactly 0.

Why -1e9 Instead of -inf?¶

You might wonder: “Why use -1e9 instead of -float('inf')?”

The practical reasons:

Numerical Stability: In some cases, having actual infinity values can cause NaN (Not a Number) issues during backpropagation. While -inf works in many cases, -1e9 is safer.
Mixed Precision Training: When using FP16 (16-bit floating point), infinity values can behave unexpectedly. A large finite number like -1e9 avoids these edge cases.
Debugging: Finite values make it easier to debug—you can inspect the actual numbers rather than seeing inf everywhere.

Why it works:

$e^{-1000000000} \approx 0$ for all practical purposes
After softmax, this becomes effectively 0.0 in the probability distribution
The difference between $e^{-1e9}$ and $e^{-\infty}$ is negligible (both round to 0)

Part 3: Visualizing the Triangle¶

In math terms, we want a Lower Triangular Matrix.

sz = 6
mask = torch.tril(torch.ones(sz, sz))

fig, ax = plt.subplots(figsize=(6, 6))
ax.imshow(mask, cmap='Greys')

# Add text labels
for i in range(sz):
    for j in range(sz):
        val = "Visible" if mask[i,j] == 1 else "Masked"
        color = "white" if mask[i,j] == 1 else "black"
        ax.text(j, i, val, ha='center', va='center', color=color, fontweight='bold')

ax.set_title("Causal Mask (Lower Triangular)")
ax.set_xlabel("Keys (Every word in sentence)")
ax.set_ylabel("Queries (Current word being processed)")
plt.show()

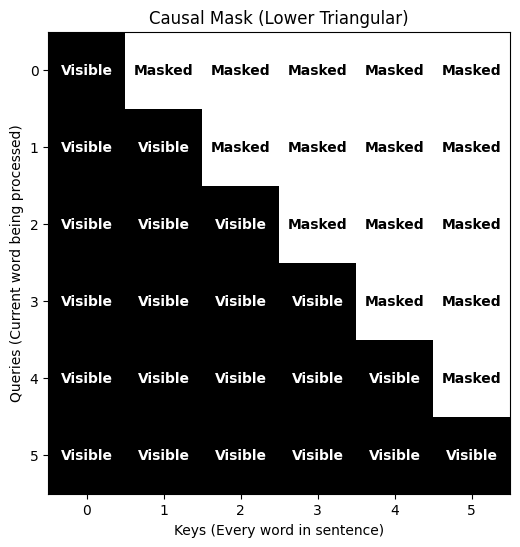
Part 4: Training vs. Inference - Why the Difference?¶

A common question: “Why do we need the causal mask during training but not during inference?”

The answer lies in how the model processes sequences in these two scenarios:

During Training (Parallel Processing)¶

Input:  "The cat sat on the"
Target: "cat sat on the mat"

What happens:

The entire sequence is fed to the model at once (parallel processing for efficiency)
At position 0, the model predicts “cat”
At position 1, the model predicts “sat”
At position 2, the model predicts “on”
...all simultaneously in one forward pass

The problem: Without masking, when predicting position 2 (“on”), the model can see positions 3, 4, 5 (“the mat”). It would just copy the answer!

Solution: The causal mask prevents position $i$ from attending to positions $> i$ , forcing the model to learn to predict from context alone.

During Inference (Sequential Generation)¶

Prompt: "The cat sat"
Step 1: Generate "on"   → "The cat sat on"
Step 2: Generate "the"  → "The cat sat on the"
Step 3: Generate "mat"  → "The cat sat on the mat"

What happens:

The model generates one token at a time
When generating token $t$ , tokens $t+1, t+2, ...$ literally don’t exist yet
We feed the growing sequence back into the model for each new token

Why no mask needed: The “future” tokens aren’t in the input at all—they haven’t been generated yet! The sequential nature of generation provides implicit causality.

Technical note: Some inference implementations still apply the mask for code simplicity and consistency with training, but it’s technically redundant since future positions are absent.

Visual Comparison¶

Training (Parallel):                  Inference (Sequential):
Input: "The cat sat on the mat"      Step 1: Input: "The cat"
                                             Output: "sat"
Position 0: sees only "The"
Position 1: sees "The cat"           Step 2: Input: "The cat sat"
Position 2: sees "The cat sat"               Output: "on"
... (all computed at once)
                                      Step 3: Input: "The cat sat on"
↑ MASK REQUIRED                              Output: "the"
  (otherwise cheating!)
                                      ↑ NO MASK NEEDED
                                        (future tokens don't exist!)

Part 5: Implementation from Scratch¶

In PyTorch, we use torch.tril (triangular lower) to create this mask. We then use masked_fill to inject the negative infinities.

def create_causal_mask(size):
    # Create a square matrix of ones, then keep only the lower triangle
    mask = torch.tril(torch.ones(size, size)).type(torch.bool)
    return mask

# Inside the Attention Forward Pass:
def forward(self, q, k, v):
    scores = torch.matmul(q, k.transpose(-2, -1)) / self.scale
    
    # Create the mask: [seq_len, seq_len]
    mask = create_causal_mask(q.size(-2)).to(q.device)
    
    # Fill "False" positions with -infinity
    # Use -1e9 instead of float('-inf') for numerical stability
    scores = scores.masked_fill(mask == 0, -1e9)
    
    attn = torch.softmax(scores, dim=-1)
    return torch.matmul(attn, v)

Summary¶

Causal Masking is required for generative models (Decoders) to prevent them from “seeing the future” during training.
The Lower Triangle: Only allows word to look at words .
Softmax Compatibility: We use a large negative value so that the Softmax operation turns those connections into probability.

Next Up: L07 – Assembling the GPT. We have all the parts: Tokenizers, Embeddings, Multi-Head Attention, LayerNorm, and Masking. We are finally ready to stack them together to build a complete “from-scratch” GPT model.