Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

Apply various anomaly detection algorithms to your validated embeddings for OCSF observability data.

What you’ll learn: How to detect anomalies using vector DB only - no separate detection model required. The vector database stores embeddings and finds similar records, while different scoring algorithms (distance-based, density-based, etc.) compute anomaly scores from those similarities. All methods work directly on TabularResNet embeddings without training additional models.

Optional extension: Section 6 covers LSTM-based sequence detection for advanced use cases like multi-step anomalies (e.g., cascading failures) - this requires training a separate model and is outside the core vector DB architecture.

Key Terminology

Before diving into detection methods, let’s define the key concepts:

Overview of Anomaly Detection Methods

Once you have high-quality embeddings, you can detect anomalies using a vector database as the central retrieval layer plus multiple scoring algorithms:

Core methods (no additional model training):

  1. Vector DB retrieval: k-NN similarity search for every event

  2. Density-based: Local Outlier Factor (LOF) on neighbor sets

  3. Tree-based: Isolation Forest (optional baseline)

  4. Distance-based: k-NN distance (cosine, Euclidean, negative inner product)

  5. Clustering-based: Distance from cluster centroids

Optional advanced method (requires separate model): 6. Sequence-based: Multi-record anomalies using LSTM (for cascading failures, correlated issues)

Each method has different strengths. We’ll implement all of them and compare.

1. Vector DB Retrieval (Central Layer)

The vector database is the system of record for embeddings. For each incoming event:

  1. Generate the embedding with TabularResNet.

  2. Query the vector DB for k nearest neighbors.

  3. Compute anomaly scores from neighbor distances or density.

  4. Persist the new embedding for future comparisons (if it’s not an outlier).

# Pseudocode interface for a vector DB client
def retrieve_neighbors(vector_db, embedding, k=20):
    """
    Query the vector database for nearest neighbors.

    Returns:
        neighbors: list of (neighbor_id, distance)
    """
    return vector_db.search(embedding, top_k=k)

def score_from_neighbors(neighbors, percentile=95):
    """
    Basic distance-based scoring from neighbor distances.
    """
    distances = [d for _, d in neighbors]
    threshold = np.percentile(distances, percentile)
    score = np.mean(distances)
    return score, threshold

# Example usage
neighbors = retrieve_neighbors(vector_db, embedding, k=20)
score, threshold = score_from_neighbors(neighbors, percentile=95)
is_anomaly = score > threshold

Scaling Notes: FAISS vs Distributed Vector DBs

2. Local Outlier Factor (LOF)

What is LOF? Local Outlier Factor measures how isolated a point is compared to its local neighborhood. Instead of using global distance thresholds, LOF compares each point’s density to its neighbors’ density.

The key insight: An anomaly isn’t just “far away” - it’s in a less dense region than its neighbors. A point can be far from cluster centers but still be normal if its local area has similar density.

How it works:

  1. For each point, find its k nearest neighbors

  2. Compute the local reachability density (how tightly packed the neighborhood is)

  3. Compare this density to the neighbors’ densities

  4. Points in sparser regions get high LOF scores (> 1 = outlier)

When to use LOF:

Advantages for OCSF observability data:

Disadvantages:

Interpretation:

import logging
import warnings

logging.getLogger("matplotlib.font_manager").setLevel(logging.ERROR)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
from sklearn.metrics import precision_score, recall_score, f1_score, confusion_matrix

def detect_anomalies_lof(embeddings, contamination=0.1, n_neighbors=20):
    """
    Detect anomalies using Local Outlier Factor.

    Args:
        embeddings: (num_samples, embedding_dim) array
        contamination: Expected proportion of anomalies
        n_neighbors: Number of neighbors for density estimation

    Returns:
        predictions: -1 for anomalies, 1 for normal
        scores: Negative outlier factor (more negative = more anomalous)
    """
    lof = LocalOutlierFactor(n_neighbors=n_neighbors, contamination=contamination)
    predictions = lof.fit_predict(embeddings)

    # Negative outlier scores (use negative_outlier_factor_)
    scores = lof.negative_outlier_factor_

    return predictions, scores

# Simulate embeddings with anomalies
np.random.seed(42)

# Normal data: 3 clusters
normal_cluster1 = np.random.randn(200, 256) * 0.5
normal_cluster2 = np.random.randn(200, 256) * 0.5 + 3.0
normal_cluster3 = np.random.randn(200, 256) * 0.5 - 3.0
normal_embeddings = np.vstack([normal_cluster1, normal_cluster2, normal_cluster3])

# Anomalies: scattered outliers
anomaly_embeddings = np.random.uniform(-8, 8, (60, 256))

all_embeddings = np.vstack([normal_embeddings, anomaly_embeddings])
true_labels = np.array([0]*600 + [1]*60)  # 0=normal, 1=anomaly

# Detect anomalies
predictions, scores = detect_anomalies_lof(all_embeddings, contamination=0.1, n_neighbors=20)

# Convert predictions: -1 (anomaly) → 1, 1 (normal) → 0
predicted_labels = (predictions == -1).astype(int)

# Evaluate
precision = precision_score(true_labels, predicted_labels)
recall = recall_score(true_labels, predicted_labels)
f1 = f1_score(true_labels, predicted_labels)

print(f"Local Outlier Factor (LOF) Results:")
print(f"  Precision: {precision:.3f}")
print(f"  Recall:    {recall:.3f}")
print(f"  F1-Score:  {f1:.3f}")
print(f"\nInterpretation:")
print(f"  Precision = {precision:.1%} of flagged items are true anomalies")
print(f"  Recall = {recall:.1%} of true anomalies were detected")
Local Outlier Factor (LOF) Results:
  Precision: 0.909
  Recall:    1.000
  F1-Score:  0.952

Interpretation:
  Precision = 90.9% of flagged items are true anomalies
  Recall = 100.0% of true anomalies were detected

Visualizing LOF Results

from sklearn.manifold import TSNE

# Reduce to 2D for visualization
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
embeddings_2d = tsne.fit_transform(all_embeddings)

# Plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# Ground truth
ax1.scatter(embeddings_2d[true_labels==0, 0], embeddings_2d[true_labels==0, 1],
            c='blue', alpha=0.6, label='Normal', s=30)
ax1.scatter(embeddings_2d[true_labels==1, 0], embeddings_2d[true_labels==1, 1],
            c='red', alpha=0.8, label='Anomaly', s=50, marker='x')
ax1.set_title('Ground Truth', fontsize=13, fontweight='bold')
ax1.legend()
ax1.grid(True, alpha=0.3)

# LOF predictions
ax2.scatter(embeddings_2d[predicted_labels==0, 0], embeddings_2d[predicted_labels==0, 1],
            c='blue', alpha=0.6, label='Predicted Normal', s=30)
ax2.scatter(embeddings_2d[predicted_labels==1, 0], embeddings_2d[predicted_labels==1, 1],
            c='red', alpha=0.8, label='Predicted Anomaly', s=50, marker='x')
ax2.set_title(f'LOF Predictions (F1={f1:.3f})', fontsize=13, fontweight='bold')
ax2.legend()
ax2.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()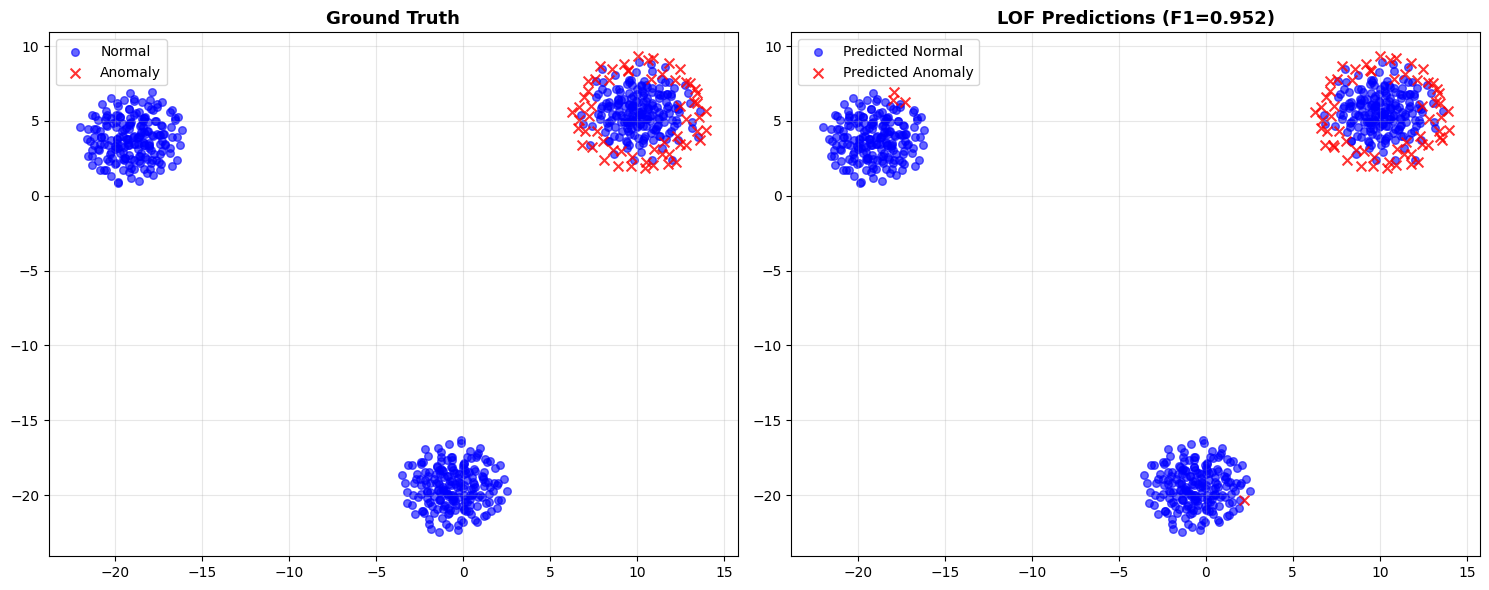
<Figure size 1500x600 with 2 Axes>

3. Isolation Forest

What is Isolation Forest? An ensemble method that isolates anomalies by building random decision trees. The key insight: anomalies are easier to isolate than normal points, requiring fewer random splits.

The intuition: Imagine randomly drawing lines to separate points. An outlier far from clusters gets isolated quickly (few splits), while a normal point in a dense cluster needs many splits to isolate.

How it works:

  1. Build 100 random trees (n_estimators=100), each selecting random features and split points

  2. For each point, measure its average path length (number of splits to isolate it)

  3. Shorter paths = easier to isolate = likely anomaly

  4. Score is normalized: values close to -1 are anomalies, close to 0 are normal

When to use Isolation Forest:

Advantages for OCSF observability data:

Disadvantages:

Hyperparameter tuning:

For observability data: Isolation Forest works well as a first pass to catch obvious outliers before applying more expensive methods like LOF.

from sklearn.ensemble import IsolationForest

def detect_anomalies_iforest(embeddings, contamination=0.1, n_estimators=100):
    """
    Detect anomalies using Isolation Forest.

    Args:
        embeddings: Embedding vectors
        contamination: Expected proportion of anomalies
        n_estimators: Number of trees

    Returns:
        predictions, scores
    """
    iforest = IsolationForest(
        contamination=contamination,
        n_estimators=n_estimators,
        random_state=42,
        n_jobs=-1
    )

    predictions = iforest.fit_predict(embeddings)
    scores = iforest.score_samples(embeddings)  # Lower = more anomalous

    return predictions, scores

# Detect anomalies
predictions_if, scores_if = detect_anomalies_iforest(all_embeddings, contamination=0.1)

# Convert predictions
predicted_labels_if = (predictions_if == -1).astype(int)

# Evaluate
precision_if = precision_score(true_labels, predicted_labels_if)
recall_if = recall_score(true_labels, predicted_labels_if)
f1_if = f1_score(true_labels, predicted_labels_if)

print(f"Isolation Forest Results:")
print(f"  Precision: {precision_if:.3f}")
print(f"  Recall:    {recall_if:.3f}")
print(f"  F1-Score:  {f1_if:.3f}")
Isolation Forest Results:
  Precision: 0.909
  Recall:    1.000
  F1-Score:  0.952

4. Distance-Based Methods

k-NN Distance

What is k-NN distance? A simple but effective method: compute the distance from each point to its k-th nearest neighbor. Points far from their neighbors are anomalies.

The intuition: Normal OCSF events have similar historical events nearby (e.g., previous logins by same user). Anomalies don’t have similar neighbors, so their k-NN distance is large.

How it works:

  1. For each event embedding, find k nearest neighbors in vector DB

  2. Compute distance to the k-th neighbor (not 1st, to avoid noise)

  3. Set a threshold (e.g., 90th percentile of all distances)

  4. Events with distance > threshold are anomalies

Why k-th neighbor, not 1st?

When to use k-NN distance:

Advantages for OCSF observability data:

Disadvantages:

Hyperparameter tuning:

Distance metrics (supported by vector DBs):

Interpretation:

For observability data: k-NN distance is the most common production method because it:

  1. Leverages existing vector DB infrastructure

  2. Provides intuitive explanations for operations teams

  3. Scales to millions of events with approximate nearest neighbor search

from sklearn.neighbors import NearestNeighbors

def detect_anomalies_knn(embeddings, k=5, threshold_percentile=90):
    """
    Detect anomalies using k-NN distance.

    Args:
        embeddings: Embedding vectors
        k: Number of nearest neighbors
        threshold_percentile: Percentile for anomaly threshold

    Returns:
        predictions, scores
    """
    # Fit k-NN
    nbrs = NearestNeighbors(n_neighbors=k+1)  # +1 because point itself is included
    nbrs.fit(embeddings)

    # Compute distances to k-th nearest neighbor
    distances, indices = nbrs.kneighbors(embeddings)
    knn_distances = distances[:, -1]  # Distance to k-th neighbor

    # Threshold: anomalies are in top (100-threshold_percentile)%
    threshold = np.percentile(knn_distances, threshold_percentile)
    predictions = (knn_distances > threshold).astype(int)

    return predictions, knn_distances

# Detect anomalies
predicted_labels_knn, scores_knn = detect_anomalies_knn(all_embeddings, k=5, threshold_percentile=90)

# Evaluate
precision_knn = precision_score(true_labels, predicted_labels_knn)
recall_knn = recall_score(true_labels, predicted_labels_knn)
f1_knn = f1_score(true_labels, predicted_labels_knn)

print(f"k-NN Distance Results:")
print(f"  Precision: {precision_knn:.3f}")
print(f"  Recall:    {recall_knn:.3f}")
print(f"  F1-Score:  {f1_knn:.3f}")
k-NN Distance Results:
  Precision: 0.909
  Recall:    1.000
  F1-Score:  0.952

4. Supported Similarity Metrics

For vector DB–driven retrieval, stick to metrics supported by VAST Vector DB:

Use one of these metrics consistently across indexing, retrieval, and scoring to keep anomaly thresholds stable.

5. Clustering-Based Anomaly Detection

What is clustering-based detection? First cluster your embeddings into groups (e.g., k-means), then flag points far from any cluster centroid as anomalies.

The intuition: Normal OCSF events form natural clusters (login events, file access, network connections, etc.). Anomalies don’t fit into any cluster and appear far from all centroids.

How it works:

  1. Run k-means clustering on historical embeddings (e.g., k=5 clusters)

  2. For each event, compute distance to nearest cluster centroid

  3. Events far from all centroids (> 95th percentile) are anomalies

  4. Can update clusters periodically (weekly) as data distribution shifts

When to use clustering-based detection:

Advantages for OCSF observability data:

Disadvantages:

Hyperparameter tuning:

Cluster interpretation for observability:

Combining with other methods:

Operational considerations:

For observability data: Clustering works well as a pre-filter before expensive methods, or when you want explainable clusters that map to known event types.

from sklearn.cluster import KMeans

def detect_anomalies_clustering(embeddings, n_clusters=3, threshold_percentile=95):
    """
    Detect anomalies as points far from cluster centroids.

    Args:
        embeddings: Embedding vectors
        n_clusters: Number of clusters
        threshold_percentile: Distance percentile for anomaly threshold

    Returns:
        predictions, scores
    """
    # Fit k-means
    kmeans = KMeans(n_clusters=n_clusters, random_state=42, n_init=10)
    kmeans.fit(embeddings)

    # Compute distance to nearest cluster centroid
    distances_to_centroids = np.min(kmeans.transform(embeddings), axis=1)

    # Threshold
    threshold = np.percentile(distances_to_centroids, threshold_percentile)
    predictions = (distances_to_centroids > threshold).astype(int)

    return predictions, distances_to_centroids

# Detect anomalies
predicted_labels_cluster, scores_cluster = detect_anomalies_clustering(
    all_embeddings, n_clusters=3, threshold_percentile=95
)

# Evaluate
precision_cluster = precision_score(true_labels, predicted_labels_cluster)
recall_cluster = recall_score(true_labels, predicted_labels_cluster)
f1_cluster = f1_score(true_labels, predicted_labels_cluster)

print(f"Clustering-Based Results:")
print(f"  Precision: {precision_cluster:.3f}")
print(f"  Recall:    {recall_cluster:.3f}")
print(f"  F1-Score:  {f1_cluster:.3f}")
Clustering-Based Results:
  Precision: 1.000
  Recall:    0.550
  F1-Score:  0.710

6. Multi-Record Sequence Anomaly Detection (Optional - Advanced)

Note: This section covers an optional advanced technique that goes beyond the core “vector DB only” architecture described in this series.

When to Use This Approach

The methods above (LOF, Isolation Forest, k-NN, clustering) detect anomalies in individual events using vector DB similarity search. However, some anomalies only appear when looking at sequences of events:

Use cases for sequence-based detection:

Trade-offs

Advantages:

Disadvantages:

Recommendation: Start with vector DB methods (Sections 1-5). For cascading failure detection:

Alternative: Agentic Multi-Step Detection

For most teams, the agentic approach in Part 9 is preferable to LSTM for detecting cascading failures:

Why agentic approach is better:

When to use LSTM instead:

See Part 9: Agentic Sequence Investigation for the recommended approach.

LSTM Implementation (Optional)

For teams that need ultra-low latency or have specific requirements for neural sequence modeling:

For detecting anomalies across sequences of events (e.g., cascading operational failures).

import torch
import torch.nn as nn

class SequenceAnomalyDetector(nn.Module):
    """
    Detect anomalies in sequences of events using embeddings.
    """
    def __init__(self, embedding_dim, hidden_dim=128):
        super().__init__()

        # LSTM to model sequences of embeddings
        self.lstm = nn.LSTM(embedding_dim, hidden_dim, num_layers=2,
                           batch_first=True, dropout=0.1)

        # Predict "normality score"
        self.scorer = nn.Sequential(
            nn.Linear(hidden_dim, 64),
            nn.ReLU(),
            nn.Linear(64, 1),
            nn.Sigmoid()  # Output probability of being normal
        )

    def forward(self, sequence_embeddings):
        """
        Args:
            sequence_embeddings: (batch_size, sequence_length, embedding_dim)

        Returns:
            normality_scores: (batch_size,) probability of sequence being normal
        """
        # Process sequence
        lstm_out, (hidden, cell) = self.lstm(sequence_embeddings)

        # Use final hidden state for scoring
        score = self.scorer(hidden[-1])

        return score.squeeze()

# Example usage
sequence_detector = SequenceAnomalyDetector(embedding_dim=256, hidden_dim=128)

# Simulate a sequence of 10 events
sequence = torch.randn(1, 10, 256)  # 1 sequence, 10 events, 256-dim embeddings
normality_score = sequence_detector(sequence)

print(f"\nSequence Anomaly Detection:")
print(f"  Sequence shape: {sequence.shape}")
print(f"  Normality score: {normality_score.item():.3f}")
print(f"  Interpretation: Lower score = more likely anomaly sequence")
print(f"\nUse case: Detect cascading failures or performance degradation patterns")

Sequence Anomaly Detection:
  Sequence shape: torch.Size([1, 10, 256])
  Normality score: 0.503
  Interpretation: Lower score = more likely anomaly sequence

Use case: Detect cascading failures or performance degradation patterns

7. Method Comparison

Why compare methods? Each anomaly detection algorithm (LOF, Isolation Forest, k-NN, Clustering) has different strengths and weaknesses. A systematic comparison on your specific OCSF data tells you which method works best for your operational patterns.

What this section does:

How to interpret results:

Typical results for OCSF observability data:

Next steps after comparison: Use the winning method’s threshold tuning (Section 8) to optimize for your team’s precision/recall priorities.

def compare_anomaly_methods(embeddings, true_labels):
    """
    Compare all anomaly detection methods.

    Args:
        embeddings: Embedding vectors
        true_labels: Ground truth (0=normal, 1=anomaly)

    Returns:
        Comparison DataFrame
    """
    results = []

    # LOF
    pred_lof, _ = detect_anomalies_lof(embeddings, contamination=0.1)
    pred_lof = (pred_lof == -1).astype(int)
    results.append({
        'Method': 'Local Outlier Factor',
        'Precision': precision_score(true_labels, pred_lof),
        'Recall': recall_score(true_labels, pred_lof),
        'F1-Score': f1_score(true_labels, pred_lof)
    })

    # Isolation Forest
    pred_if, _ = detect_anomalies_iforest(embeddings, contamination=0.1)
    pred_if = (pred_if == -1).astype(int)
    results.append({
        'Method': 'Isolation Forest',
        'Precision': precision_score(true_labels, pred_if),
        'Recall': recall_score(true_labels, pred_if),
        'F1-Score': f1_score(true_labels, pred_if)
    })

    # k-NN Distance
    pred_knn, _ = detect_anomalies_knn(embeddings, k=5)
    results.append({
        'Method': 'k-NN Distance',
        'Precision': precision_score(true_labels, pred_knn),
        'Recall': recall_score(true_labels, pred_knn),
        'F1-Score': f1_score(true_labels, pred_knn)
    })

    # Clustering
    pred_cluster, _ = detect_anomalies_clustering(embeddings, n_clusters=3)
    results.append({
        'Method': 'Clustering-Based',
        'Precision': precision_score(true_labels, pred_cluster),
        'Recall': recall_score(true_labels, pred_cluster),
        'F1-Score': f1_score(true_labels, pred_cluster)
    })

    # Sort by F1-Score
    results = sorted(results, key=lambda x: x['F1-Score'], reverse=True)

    # Print comparison table
    print("\n" + "="*70)
    print("ANOMALY DETECTION METHOD COMPARISON")
    print("="*70)
    print(f"{'Rank':<6} {'Method':<25} {'Precision':<12} {'Recall':<12} {'F1-Score':<12}")
    print("-"*70)
    for i, r in enumerate(results, 1):
        print(f"{i:<6} {r['Method']:<25} {r['Precision']:<12.3f} {r['Recall']:<12.3f} {r['F1-Score']:<12.3f}")
    print("="*70)

    return results

# Run comparison
comparison_results = compare_anomaly_methods(all_embeddings, true_labels)

======================================================================
ANOMALY DETECTION METHOD COMPARISON
======================================================================
Rank   Method                    Precision    Recall       F1-Score    
----------------------------------------------------------------------
1      Local Outlier Factor      0.909        1.000        0.952       
2      Isolation Forest          0.909        1.000        0.952       
3      k-NN Distance             0.909        1.000        0.952       
4      Clustering-Based          1.000        0.550        0.710       
======================================================================

8. Threshold Tuning

Why threshold tuning matters: All anomaly detection methods require setting a threshold - the cutoff between “normal” and “anomaly”. Too low → miss operational issues (low recall). Too high → false alarms (low precision).

The challenge: Operations teams have different priorities:

Precision-Recall trade-off:

Example scenarios:

  1. Critical services (payment processing): High recall (95%) > precision. Can’t miss performance degradation.

  2. Log analysis (general monitoring): Balanced (F1 score). Limited investigation capacity.

  3. Alert fatigue prevention: High precision (90%) > recall. Operations team overwhelmed by alerts.

Precision-Recall Curve

What is a PR curve? A plot showing precision vs recall at different thresholds. Use it to visualize the trade-off and select the optimal threshold for your operations team’s priorities.

How to read it:

Interpretation:

For observability data: Choose threshold based on your investigation capacity:

from sklearn.metrics import precision_recall_curve, auc

def plot_precision_recall_curve(true_labels, scores, method_name):
    """
    Plot precision-recall curve for threshold tuning.

    Args:
        true_labels: Ground truth
        scores: Anomaly scores (higher = more anomalous)
        method_name: Name of the method
    """
    precision, recall, thresholds = precision_recall_curve(true_labels, scores)
    pr_auc = auc(recall, precision)

    plt.figure(figsize=(8, 6))
    plt.plot(recall, precision, linewidth=2, label=f'{method_name} (AUC={pr_auc:.3f})')
    plt.xlabel('Recall', fontsize=12)
    plt.ylabel('Precision', fontsize=12)
    plt.title(f'Precision-Recall Curve: {method_name}', fontsize=14, fontweight='bold')
    plt.legend()
    plt.grid(True, alpha=0.3)
    plt.tight_layout()
    plt.show()

    print(f"\nPrecision-Recall AUC: {pr_auc:.3f}")
    print(f"Use this curve to select the best threshold for your use case")

# Example: Plot PR curve for k-NN distance
plot_precision_recall_curve(true_labels, scores_knn, "k-NN Distance")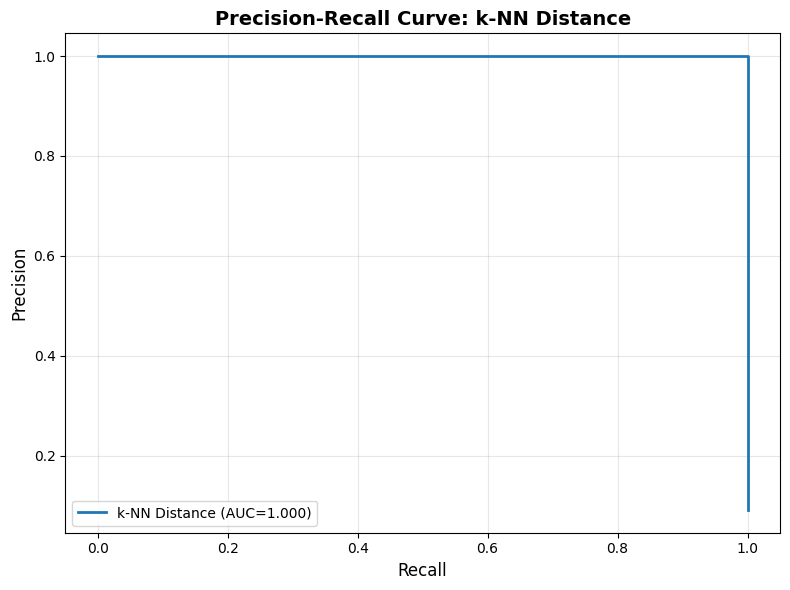
<Figure size 800x600 with 1 Axes>

Precision-Recall AUC: 1.000
Use this curve to select the best threshold for your use case

9. Production Pipeline

Why a production pipeline matters: Combining all the pieces (preprocessing, embedding generation, anomaly detection, alerting) into a single, deployable system.

The end-to-end flow:

  1. Ingest: Receive OCSF events from log collectors (Splunk, Kafka, etc.)

  2. Preprocess: Extract features, apply scaler/encoders from Part 3

  3. Embed: Generate 256-dim embedding using trained TabularResNet

  4. Retrieve: Query vector DB for k nearest neighbors

  5. Score: Apply anomaly detection algorithm (LOF, k-NN, etc.)

  6. Alert: If score > threshold, send to SIEM/ticketing system

  7. Store: Persist embedding in vector DB for future comparisons (if not anomaly)

Key design decisions:

  1. Stateful vs Stateless:

    • Stateful (LOF, Isolation Forest): Pre-fitted on historical data, used for prediction

    • Stateless (k-NN distance): No pre-fitting, query vector DB directly

    • Recommendation: Start with stateless k-NN (simpler, scales better)

  2. Online vs Batch:

    • Online (real-time): Process each event as it arrives (<100ms latency)

    • Batch (offline): Process events in batches every 5 minutes

    • Observability context: Most operational issues span minutes/hours, so 5-min batches are acceptable

  3. Novelty detection mode:

    • Fit once on clean historical data (normal events only)

    • Predict on new events (don’t retrain on anomalies)

    • LOF novelty=True enables this mode for streaming data

  4. Error handling:

    • Missing features → use defaults or skip (don’t crash pipeline)

    • Model timeout → fall back to rule-based detection

    • Vector DB down → buffer events, replay when recovered

Operational monitoring:

For observability data: Production pipeline must be reliable (no events dropped), fast (detect issues within minutes), and explainable (provide context for each alert).

Complete Anomaly Detection Pipeline

What this code provides: A reusable class that wraps TabularResNet + preprocessing + anomaly detection, ready for integration with your observability infrastructure.

class AnomalyDetectionPipeline:
    """
    Production-ready anomaly detection pipeline.
    """
    def __init__(self, model, scaler, encoders, method='lof', contamination=0.1):
        """
        Args:
            model: Trained TabularResNet
            scaler: Fitted StandardScaler for numerical features
            encoders: Dict of LabelEncoders for categorical features
            method: 'lof', 'iforest', 'knn', or 'ensemble'
            contamination: Expected anomaly rate
        """
        self.model = model
        self.scaler = scaler
        self.encoders = encoders
        self.method = method
        self.contamination = contamination
        self.detector = None

    def fit(self, embeddings):
        """Fit the anomaly detector on normal data."""
        if self.method == 'lof':
            self.detector = LocalOutlierFactor(
                n_neighbors=20,
                contamination=self.contamination,
                novelty=True  # For online prediction
            )
        elif self.method == 'iforest':
            self.detector = IsolationForest(
                contamination=self.contamination,
                random_state=42,
                n_jobs=-1
            )
        elif self.method == 'knn':
            self.detector = NearestNeighbors(n_neighbors=5)

        self.detector.fit(embeddings)
        print(f"Anomaly detector ({self.method}) fitted on {len(embeddings)} samples")

    def predict(self, ocsf_records):
        """
        Predict anomalies for new OCSF records.

        Args:
            ocsf_records: List of OCSF dictionaries or DataFrame

        Returns:
            predictions: Binary array (1=anomaly, 0=normal)
            scores: Anomaly scores
        """
        # TODO: Implement preprocessing and embedding extraction
        # This is a simplified example
        pass

print("AnomalyDetectionPipeline class defined")
print("Usage:")
print("  pipeline = AnomalyDetectionPipeline(model, scaler, encoders, method='lof')")
print("  pipeline.fit(training_embeddings)")
print("  predictions, scores = pipeline.predict(new_ocsf_records)")
AnomalyDetectionPipeline class defined
Usage:
  pipeline = AnomalyDetectionPipeline(model, scaler, encoders, method='lof')
  pipeline.fit(training_embeddings)
  predictions, scores = pipeline.predict(new_ocsf_records)

Summary

In this part, you learned:

  1. Core vector DB approach: Five scoring algorithms (LOF, Isolation Forest, k-NN, clustering) that work directly on TabularResNet embeddings—no additional model training required

  2. Method comparison framework for selecting the best approach

  3. Threshold tuning using precision-recall curves

  4. Production pipeline for real-time anomaly detection

  5. Optional advanced extension: LSTM-based sequence anomaly detection for cascading failures (requires training a separate model)

Key Takeaways:

Next: In Part 7, we’ll deploy this system to production with REST APIs for embedding model serving and integration with observability platforms.

Advanced Extension: For production systems with multiple observability data sources (logs, metrics, traces, configuration changes), see Part 9: Multi-Source Correlation to learn how to correlate anomalies across sources and automatically identify root causes.

References

Embedding-Based Anomaly Detection for Observability
Part 5: Evaluating Embedding Quality
Embedding-Based Anomaly Detection for Observability
Part 7: Production Deployment